BSE bulk solids engineering Tel.: +31 53 434 45 66
Print: 02 Mar 2026 01:37



BulktechnologieEigenschappen, metingen, ontwerpen, fenomenen in ons vakgebiedHieronder staat een samenvoeging van verschillende artikelen en bijdragen in de media over het vakgebied van de bulktechnologie. Allereerst een definitie van de stof waar we het over hebben. Dan een schets van het werkgebied en de problemen die we tegenkomen. Vervolgens worden per hoofdstuk steeds een onderwerp uit het vakgebied behandeld. I N H O U D
Naamgeving: Stortgoed, bulk of solids?
Definitie van de stof waar het om gaat
Bulk solids, Stortgoed, Poeder, Granulaat, Korrels, Engelse termen, Bulk, Solids WerkgebiedWaar vinden we bulk solids?
Technische definitie, Verliespost industrie, Deeltjestechnologie en bulktechnologie. Bulk solids heeft vele gezichtenWat maakt bulk solids zo speciaal, en lastig?
Inleiding, Traditie, Transportapparatuur, Bulkgoedeigenschappen, Praktische bruikbaarheid, Wandwrijving, Inwendige wrijving, Geen vloeistof, Consolidatie, Cohesie, Invloed van vocht StortgoedkarakteriseringMethoden voor meting van bulkgoedeigenschappen in de industrie
Indelingen, Soorten loopgedrag, Oorzaak van verschillen in loopgedrag, Porositeit, Deeltjesgrootte, Deeltjesvorm, Deeltjessterkte, Attritie, Deeltjesdichtheid, Bulkdichtheid, Hausner Ratio, Pyknometer Meting stromingsgedragMeting van mechanische eigenschappen (loopeigenschappen)
Bewegingssnelheid, Afschuiftesters (shear cells), Meting bezwijklijn, Tijdsconsolidatie, Wandwrijvingsmeting Jenike shear cellIn de praktijk blijkt de Jenike shearcell meestal het best bruikbaar
Product-eigenschappen; Mechanische eigenschappen; Meetprocedure; Alternatieve testers; Verwerking resultaten Wandwrijving in de bulktechnologieWaar treedt het op, en hoe kunnen we het meten
Wandwrijving bij silo-opslag, mechanisch transport, pneumatisch transport en andere bewerkingen; Factoren die de wandwrijving bepalen; Meten van de wandwrijving, wandwrijving in damwandsilo's. Wandwrijvingsmeting van stortgoedMeting toch niet zo simpel als het lijkt
Europese Werkgroep voor wandwrijvingsmetingen door 13 laboratoria wereldwijd; Testprocedure wandwrijvingsmeting; Praktische bruikbaarheid voor silo-ontwerp en drukberekening. Stroming uit silo’s gaat niet vanzelfStromingstechnieken moeten de basis vormen van elk ontwerp
Ontwikkeling bulkhandling; Silogeometrie, Slanke silo’s, Mammoetsilo's, platbodemsilo's; Stromingspatronen, Massastroming, Kernstroming; Trechtervormen, Axiaalsymmetrische stroming, Vlaksymmetrische stroming, Trechterhoek; Stromingsproblemen, Brugvorming, Schachtvorming, Tijdsconsolidatie. Silo-ontwerp; MassastromingDoel: massastroming door zwaartekracht in een eenvoudige silo
Siloontwerp is maatwerk; Stromingspatroon, Massastroming; Invloeden stromingspatroon, Procedure massastroom-ontwerp; Ontwerp op brugvorming, Verklemming van grote brokken, Cohesieve brugvorming, Flow – No Flow, Sterkte van de brug, Procedure brugvorming; Stromingsbevordering (flow promotion), Brugbrekers, Uitdraagbodems; Uitdraagapparatuur, Uitdraagschroef (screw feeder), Richtlijnen voor uitdraagapparatuur. Silo-ontwerp en productverstevigingDe invloed van tijdsconsolidatie
Maandagochtendhumeur; Tijdsflowfunctie; Uitstroomopening na stilstand; Ontwerp met stilstand, Consolidatie breken, Uitdraagbodem, Consolidatie voorkomen; Productversteviging en stromingspatroon; Invloed van het onttrekmechanisme; Brugvorming in de cilinder Silo's met kernstromingStroomkanaal bevindt zich in product zelf bij kernstroomsilo
Kernstroming versus massastroming; Kleinere bouwhoogte; Stabiele schachtvorming vermijden, bovengrens stabiele schachtvorming, ondergrens stabiele schachtvorming; Controle op brugvorming; Trechterhoek voor leegstromen; Extended flow hopper; Platbodemsilo's of stockpiles Probleemloos doseren met een doseerschroefOntwerp op basis van minimale spoed, kerndiameter en spoedverloop
Doseerschroef, doseervijzel, uitdraagschroef, screw feeder; Werkingsprincipe schroeftransport; Optimaal schroeftransport; Minimaal toepasbare spoed; Ontwerp doseerschroef; Aandrijfvermogen Uitstroomcapaciteit uit silo’sBerekening van de uitstroomhoeveelheid van poeders en korrels
Uitstroomdebiet, massadebiet voor grofkorrelig vrijstromend stortgoed; Voor vrijstromende fijnkorrelige producten en poeders; Opvoering van het debiet door luchtinjectie; Uitstroomcapaciteit bij cohesief materiaal Meer verzamel-documenten: Fenomenen in silo'sDrukopbouw, productbreuk, silo-schokken, ontmenging
Over fenomenen die we tegenkomen bij opslag van bulkgoed in silo's, en die problemen kunnen veroorzaken. Met daarbij oplossingsrichtingen en enkele praktijkcases Belastingen in silo'sBelastingen op silowanden; EN 1991-4; Belastingen op inserts
Klassieke Janssen-formule; Geldende normen; Speciale belastingssituaties bij inbouwelementen in silo’s en storthopen. Naamgeving: Stortgoed, bulk of solids?Definitie van de stof waar het om gaatBulkgoed, bulk solids
Een verzameling vaste deeltjes ter grootte van micrometers (poeders) tot millimeters (korrels) tot centimeters (brokken), wordt in het Engels “bulk solids” genoemd.
Een “solid” is een vaste stof. Dat kan een element in vaste toestand zijn (ijzer, goud) maar ook een heel andersoortig materiaal, zoals steen, beton, of hout. Alles wat een vaste substantie heeft.
Het Engelse woord “bulk” wordt ook in het Nederlands gebruikt: ‘in bulk’ betekent in grote hoeveelheid, onverpakt. Een definitie voor deze stof kan zijn: een hoeveelheid deeltjes, die in principe vrij kunnen bewegen, maar een duidelijke interactie vertonen en tevens beïnvloed worden door in of tussen deze deeltjes aanwezige gassen en/of vloeistoffen. 
StortgoedDe term bulk solids wordt dus vertaald als vaste stoffen in bulk, ofwel onverpakte vaste stoffen. In het Nederlands is de correcte, maar enigszins wetenschappelijke, vertaling: stortgoed. Het is een stof, een materiaal, dat gestort kan worden. Hierbij moeten we storten zien als vullen, schenken, zoals een pudding gestort kan worden. Deze term ligt dicht bij het Duitse Schüttgut, waar ‘schütten’ ook inderdaad schenken betekent. Toen het onderzoeksgebied aan de Universiteit Twente, destijds nog TH, werd opgezet, werd dit stortgoedtechnologie genoemd, de opleiding tot stortgoedtechnoloog. In de loop van de tijd heeft storten vooral de betekenis gekregen van afval storten, met daarbij een extra negatieve klank door illegale praktijken. In het woordenboek staat bij stort: het storten, gifstort. En als tweede: de vuilstort. Producenten en verwerkers willen niet dat hun grondstof of (half)product wordt geassocieerd met afvalstoffen. Vandaar dat vaak andere benamingen worden gebruikt: droge stof, vaste stoffen, bulkgoed, solids, granulaat, aggregaat, of bulk zonder nadere aanduiding. PoederPoeder is eigenlijk een hele duidelijke aanduiding van stortgoed, waar iedereen een gevoel bij heeft. Maar een poeder is (zeer) fijnkorrelig, terwijl stortgoed ook uit grote delen kan bestaan. Granulaat, korrels, etcVaak afhankelijk van het werkgebied, wordt bulkgoed ook aangeduid als granulaat, granulaire materialen, pellets, korrels, korrelige materie, korrelvormige goederen, briketten. Bij briketten ligt ongeveer de grens tussen een vaste stof in bulk, en een ‘echte’ vaste stof. Sommige briketten worden nog als massa verwerkt. Andere briketten zijn zo groot dat ze worden opgestapeld. 

Engelse termenOok in het Engels zijn er naast bulk solids natuurlijk andere termen: bulk goods, granular media, powder, aggregates, granulates, pellets. Wanneer de nadruk meer op het gedrag en de eigenschappen van de deeltjes ligt, heeft men het over particle technology (deeltjestechnologie). In Nederland worden, zoals we gewend zijn, veelal de Engelse termen gebruikt: bulk solids voor de meer wetenschappelijke invalshoek. 
BulkDe term bulk zonder solids wordt voornamelijk gebruikt als het over grote hoeveelheden en grote productstromen gaat: scheepsladingen, treinladingen, grote silo’s, en bij lange trajecten met bandtransporteurs. Vaak wordt er gesproken over bulk handling, terwijl de correcte term binnen ons vakgebied eigenlijk bulk solids handling is. SolidsWaar de term bulk vaak over transport en opslag gaat, wordt bij verwerking vaak de term solids processing gebruikt. Het gaat dan om zgn. “unit operations” zoals mengen, breken, agglomereren, scheiden, verwarmen, koelen. Vanuit deze samenstelling wordt de term solids ook steeds meer los gebruikt, bijvoorbeeld bij de naamgeving van beurzen. Binnen het vakgebied is dit geen probleem, men weet dat het over solids als bulk gaat, over bulk solids dus. Buitenstaanders zouden wel eens op het verkeerde been gezet kunnen worden: solids zijn vaste stoffen, of vaste vormen: SolidWorks heeft niets met bulkgoed te maken. Maar ook binnen het vakgebied kan de term solids verwarrend zijn, bijvoorbeeld bij de bulkdichtheid (bulk density) versus de deeltjesdichtheid (solid density). De term solids density zou hetzelfde betekenen als bulk density, hetgeen een duidelijk andere waarde is als de solid density. TenslotteIn dit artikel gebruiken we de termen bulk solids, bulkgoed, bulk of solids, maar het blijft hetzelfde: een vaste stof in fijne of minder fijne delen die als massa (in bulk) wordt getransporteerd, verwerkt op opgeslagen. WerkgebiedWaar vinden we bulk solids?Stortgoed omvat alle materialen die bestaan uit vele afzonderlijke deeltjes, die groot genoeg zijn om niet onderhevig te zijn aan thermische beweging bij kamertemperatuur. Deze enigszins technische definitie omvat alledaagse materialen zoals zand, meel, grind, ijzererts, houtsnippers, zaagsel, etc. Soms zijn de deeltjes geheel of bijna rond, soms glad, soms ruw, met scherpe hoeken of hakerig. We kennen (graan)korrels, vlokken, krullen brokken, etc.
Verliespost industrieIn de industrie zijn de meest verwerkte producten in korrelvorm, en problemen bij de verwerking ervan veroorzaken een duizelingwekkend verlies van 5% van de in de wereld verbruikte energie (hetgeen overeenkomt met meer dan 300 miljard euro per jaar). Het mag duidelijk zijn dat kennis van het gedrag van stortgoed erg belangrijk is. Helaas wordt het gedrag van granulaire materialen nog steeds slecht begrepen. Granulaire materie kan worden bestudeerd vanuit een fundamenteel en een technisch perspectief, gewoonlijk respectievelijk aangeduid als deeltjestechnologie en bulktechnologie. Deze gebieden zijn natuurlijk sterk verweven, omdat het gedrag en de eigenschappen van het afzonderlijke deeltje invloed heeft op het samenstel van deeltjes, en vaak ook vice versa. Deeltjestechnologie en bulktechnologie.Onderwerpen in deze vakgebieden zijn:
Bulk solids heeft vele gezichtenWat maakt bulk solids zo speciaal, en lastig?Inleiding met betrekking tot de eigenschappen van bulk solids, over de geschiedenis van opslag en overslag van bulk solids en de relatie met transportwerktuigen. Inventarisatie en classificatie van bulkeigenschappen, en beschrijving van elementair gedrag: verschillen met vloeistof en invloed van cohesie en consolidatie. InleidingEen bulk solid, zelfs als het om een stof met één chemische samenstelling gaat, heeft vele gezichten. Er zijn enkele tientallen eigenschappen van bulk solids te benoemen. In een zekere situatie zal steeds een bepaalde verzameling van eigenschappen verantwoordelijk voor het wel of niet functioneren van installaties. Bij veranderde omstandigheden spelen weer andere eigenschappen een rol. Dat maakt de verwerking van bulk solids tot een lastige zaak. Inzicht in de materie is daarom nodig om problemen te vermijden. 
Over de gehele wereld worden miljarden tonnen in de vorm van bulk getransporteerd, opgeslagen en verwerkt. En het aantal producten dat de procesindustrie in bulk op de markt brengt, neemt nog steeds toe. Het transport van die grote massa's in talloze soorten vergt erg veel van onze technische mogelijkheden en verloopt niet altijd probleemloos. Vaak zijn storingen onvoorspelbaar omdat teveel onbekende, en ook niet goed achterhaalbare, factoren een rol spelen. Er zijn echter ook veel gevallen waar achteraf is aangetoond dat de moeilijkheden hadden kunnen worden voorkomen. Schaalgrootte bulk solidsDe deeltjesverzamelingen waar het bij bulktechnologie om draait, worden in de praktijk vaak op diverse manieren aangeduid.
Als stortgoed, bulkgoed, bulk solids, poeders, granulaten, en nog vele andere benamingen.
Het gaat hier dan natuurlijk niet om de elementaire deeltjes uit de fysica, noch om de zeer kleine deeltjes uit de nano-technologie.
Vele takken van industrie krijgen te maken met zeer grote hoeveelheden bulkgoederen als grondstoffen, halffabricaten en eindproducten.
TraditieHet transport van traditionele bulkgoederen zoals granen, sojabonen en steenkolen is meestal weinig problematisch. De ontwikkeling van de hiervoor bestemde transportwerktuigen heeft in de loop van eeuwen plaatsgevonden, een soort evolutie. Zo groeide om elk soort bulkgoed een eigen transportsysteem. Hoewel deze systemen dagelijks worden toegepast en goed voldoen, berust het ontwerp ervan nog vaak op empirische gegevens die vaak niet in handboeken staan. De algemene basiskennis heeft lang ontbroken, zodat het moeilijk was om op andere transportapparatuur over te gaan, of om meer geschikte transportapparatuur te ontwerpen. Ook bij de opslag van bulk solids geldt dit. Zo dachten de eerste ontwerpers dat bij de sterkteberekening van silo's kon worden aangenomen dat een bulk solid zich gedraagt als een vloeistof. Experimenten met modellen en silo's op ware grootte toonden echter aan dat de wanddrukken niet lineair met de diepte toenemen. Een deel van het bulkgewicht wordt via wrijvingskrachten op de wand overgedragen. Hierdoor zijn de drukken op bodem en wanden van een silo lager in het geval van een vloeistof met dezelfde specifieke bulkdichtheid als bij het bulkgoed. Maar de drukken langs op de wand daarentegen zijn hoger, met als gevolg dat een cilinder kan gaan plooien als de wand te dun is om de verticale krachten te kunnen dragen. Problemen met transport, opslag en verwerking van bulk solids werden steeds groter, door de excessieve toename van het aantal verschillende soorten bulk solids. Al spoedig bleek dat een groot deel daarvan niet was te vergelijken met de vrij stromende, zich goed voegende natuurproducten zoals graan, waarmee men tot 200 jaar geleden voornamelijk te maken had. Dat de handling van veel soorten bulk solids ernstige problemen oplevert, blijkt uit het grote aantal schadegevallen op dit gebied. Tegenwoordig bezwijken er in de wereld gemiddeld vijf silo's per dag. Andere grote kostenposten, zoals slecht stromende silo’s en niet of slecht werkende transportapparatuur blijven daarbij onder de radar. TransportapparatuurEen transportketen voor bulk solids bestaat in grote lijnen uit silo’s en transportapparatuur, zoals elevatoren, kettingtransporteurs, schroeftransporteurs, triltransporteurs, bandtransporteurs, grijperkranen, en verder ondersteunende apparaten, zoals weeginrichtingen, magneetscheiders en zeven, maalmolens, afzakapparatuur, etc. Door de grote variëteit in het aanbod transportapparatuur op de markt zou men kunnen denken dat deze werktuigen weinig problemen opleveren. De praktijk logenstraft deze gedachte dagelijks; problemen met transportwerktuigen zorgen voor extra en onvoorziene kosten. De functie van een transportwerktuig is, eenvoudig gezegd: verplaatsing van A naar B. Daarbij zijn drie gebieden te onderkennen: op- of innemen van het bulkgoed op plaats A; Dan transport naar plaats B, en vervolgens afgeven van het materiaal in B. De praktijk leert dat de meeste problemen optreden aan het begin en /of einde van een transportwerktuig en zelden tijdens het eigenlijke transport. BulkgoedeigenschappenNa 1960 kwam onderzoek op gang naar relevante eigenschappen van buk solids (stortgoedeigenschappen) voor transport en opslag. Zo riep het 'Research Committee of The Institution of Chemical Engineers' in 1963 een working party in het leven die zou rapporteren over de stand van onderzoek in Engeland. Dit heeft geleid tot een classificatie waarin de eigenschappen naar naam en onderwerp werden gerangschikt. Hierdoor werd alleen maar duidelijker dat het gedrag van bulk solids een uiterst gecompliceerd onderwerp vormt, dat zich nauwelijks voor een universele aanpak leent, wat nog bevestigd werd door Palowitsch e.a [1]. Zo bleek dat de volgende eigenschappen en/of invloedsgrootheden van bulk solids een significante rol kunnen spelen: Slijt- en ploegwrijving; attritie; degradatie; vriessterkte; adhesie; beluchtbaarheid en vloeibaarheid; statische taludhoek; glijhoek; bulkdichtheid; werkelijke dichtheid (solid density); cohesie; corrosiviteit; stuifgevoeligheid; hardheid; inwendige wrijving; samenstelling van de deeltjes; penetreerbaarheid; plasticiteit; poriedruk; porositeit; potentiële volumeverandering; reëel contactoppervlak; segregatie; seismische golfvoortplantingssnelheid; anisotropie; deeltjesvorm; deeltjesdistributie; deeltjesgrootte; afschuifsterkte; specifieke warmte; oppervlakte-energie; oppervlakteruwheid van de deeltjes; thermische geleidbaarheid; ongesteunde bezwijkdrukspanning; watergehalte; tussenruimtefractie en volumeverandering bij afschuiving. De meeste van deze eigenschappen worden bovendien nog beïnvloed door vocht, temperatuur en soms druk, en zijn onderhevig aan verandering in de tijd. Deze classificatie heeft dan ook geen bruikbare resultaten opgeleverd voor een algemene benadering. Praktische bruikbaarheidOp grond van terreinverkennende experimenten en fysisch inzicht, is het mogelijk gebleken de grote hoeveelheid eigenschappen te vervangen door een kortere lijst die bestaat uit drie groepen van eigenschappen die van belang zijn voor transport en opslag van bulk solids: 1) Elementaire eigenschappen van bulk solids
2) Eigenschappen van het transportwerktuig
3) Eigenschappen van bulk solids en transportwerktuig samen
Deze ordening geeft handvatten voor een praktische benadering bij ontwerp van transportapparatuur en oplossing van problemen hiermee. Voor een bepaald geval kan worden ingezoomd op eigenschappen die hier van belang zijn. We zien eigenschappen die in alle situaties van belang kunnen zijn. Zo kan de korrelgrootte betekenis hebben bij bulk solids dat uit een silo stroomt: indien de korrels klein zijn ten opzichte van de uitstroomopening, doch niet zo klein dat cohesie ontstaat, wordt het stroomgedrag nauwelijks beïnvloed. De korrelgrootte kan echter wel bepalend zijn bij (te) grote korrels, die zelfs tot blokkade kunnen leiden. Bij mechanisch transport beweegt het bulkgoed ten opzichte van de omgeving. Het kan daarbij in beweging zijn ten opzichte van de wand van het werktuig of inwendig in beweging zijn. Beide bewegingen kunnen met lage en hoge snelheden plaatsvinden en van aard verschillen. Bij de werktuigen (bijvoorbeeld bandtransporteurs) waarbij het bulkgoed niet beweegt ten opzichte van de transporteur (in dit geval: de band) treden vaak grote snelheidsverschillen op bij invoer/toevoer en uitvoer/afworp van de transporteur. Ook bij verticaal schroeftransport, waar de schroef een hoog toerental moet hebben om het product tegen de buitenwand te slingeren, zijn de snelheden hoog. Bij horizontaal schroeftransport en bijv. kettingtransporteurs (“Redlers”) zijn snelheden daarentegen laag, zeker als het werktuig ruim ontworpen is voor de gewenste capaciteit. Dit is gunstig in het kader van stofexplosiegevaar: ATEX-richtlijnen eisen dat de snelheid in transportwerktuigen beperkt blijft Wandwrijving, inwendige wrijvingTijdens transport en opslag hebben we te maken met wandwrijving en inwendige wrijving. Wandwrijving treedt op aan de “buitenkant” van het bulkgoed, daar waar bulkgoed de wand raakt. Het oppervlak is daarbij goed gedefinieerd door het transportwerktuig of de silo. Men onderscheidt statische wandwrijving, wanneer bulkgoed in beweging moet komen, en dynamische wandwrijving, wanneer het eenmaal aan het glijden is. De wandwrijving is niet of nauwelijks snelheidsafhankelijk; snelheden zijn meestal beperkt, zeker in silo’s. Bij pneumatisch transport liggen snelheden hoger, maar is er bij vliegtransport ook geen sprake meer van een bulk solid dat als samenhangend geheel langs de wand schuift Solids kunnen echter ook in zichzelf afschuiven, inwendige bewegen. De inwendige wrijving bepaalt dan hoe makkelijk die beweging is. Hier zijn drie waarde te onderscheiden: de statische inwendige wrijving (bij rust), de dynamische inwendige wrijving, wanneer deeltjes veel bewegingsvrijheid hebben, en de pseudo-statische inwendige wrijving, die optreedt bij lage vervormingsnelheden, zoals in silo’s. En die wordt beïnvloed door o.a. de heersende silodruk. Geen vloeistofMen moet zich bewust zijn dat ogenschijnlijk vloeistof-analoge stromingen zeer misleidend kunnen zijn en wel om de volgende redenen:
Ondanks de grote verschillen met een vloeistof wordt het toch vaak hiermee vergeleken. In beide gevallen gaat het immers toch vaak om het stromen van materiaal.
Toch zijn de verschillen veel groter dan deze schijnbare overeenkomst. Zie onderstaande figuur voor kenmerkend verschil,
waar de verticale druk sigmaV en de druk op de wand sigmaH zijn aangegeven voor respectievelijk een vloeistof en een bulkgoed in een cilinder.
CohesieBij het ontwerpen van apparatuur voor bulk solids, of dit nu is voor transport, opslag, overslag, verwerking of bewerking is, moet men weten of er sprake is van een vrij stromend of een cohesief bulkgoed. In het laatste geval is de mate van cohesie en/of adhesie veelal bepalend voor de selectie en dimensionering van de werktuigen, terwijl de chemische eigenschappen en/of de slijtende werking de materiaalkeuze bepalen. Bij deeltjes van nagenoeg gelijke afmetingen zal over het algemeen geen cohesief gedrag worden geconstateerd als de deeltjes groter zijn dan 1 cm. Dit komt niet omdat de deeltjes elkaar niet aantrekken, maar omdat deze krachten zo klein zijn dat ze door het eigen gewicht van de deeltjes verre worden overtroffen. Bij vermaling ontstaan kleinere deeltjes waarbij de eigen gewichtskrachten zodanig kunnen afnemen dat het omgekeerde wordt bereikt. De krachten als gevolg van het eigen gewicht van de deeltjes zijn dan te verwaarlozen in vergelijking met de cohesieve krachten tussen de deeltjes onderling. Dit laatste is in het algemeen het geval voor deeltjes kleiner dan 10 micrometer (de 'fines'). Verreweg de meeste problemen bij transport en opslag worden veroorzaakt doordat ontwerpers onvoldoende kennis hebben van bulkeigenschappen; in het bijzonder waar het de invloed van cohesie betreft. Het cohesief gedrag wordt veroorzaakt door een combinatie van de volgende verschijnselen:
De invloed van vloeistof is over het algemeen het grootst. Bij pneumatisch transport kunnen elektrostatische oplading en Van der Waalskrachten echter ook belangrijke factoren zijn. Invloed van vochtIn de praktijk blijkt dat in de meeste mechanische transporteurs en bij opslag de invloed van de vloeistofbruggen doorslaggevend is, en dat vocht bij veel soorten bulk solids een rol speelt. In onderstaande schets is aangegeven wat verschillende toestanden zijn van deeltjes met vocht. 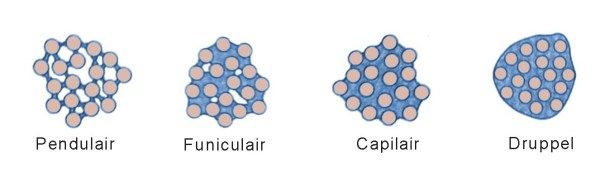
Wanneer een stortgoed in contact is met vochtige lucht kan waterdamp laagsgewijs worden geabsorbeerd. Indien echter verzadiging plaatsvindt kan condensatie plaatsvinden die voornamelijk leidt tot de formatie van vloeistof bruggen bij de contactpunten van de korrels. Bij toenemende relatieve vochtigheid zullen op meer punten vloeistofbruggen ontstaan. De poriën tussen de deeltjes zijn nog niet gevuld met vocht. Dit is de pendulaire staat. Wanneer er meer vocht wordt toegevoerd, gaat het product via de funiculaire staat (nog wel poriën vrij van vocht) naar de capillaire staat. Waarbij alle poriën gevuld zijn. Het hangt af van de grootte en hoeveelheid van de poriën, maar waarschijnlijk gedraagt het product zich in deze toestand niet meer als een bulk solid, maar meer als een dikke pasta. In de laatste toestand is er meer vocht dan deeltjes, en is het product een slurry geworden. Consolidatie
De genoemde verschillen wijzen erop dat bulk solids eerder als een plastisch dan een visco-elastisch medium zou moeten worden opgevat. Een extra complicatie vormt de gevoeligheid voor consolidatie (versteviging) van bulk solids. Deze eigenschap leidt tot een verhoging van de mechanische sterkte wanneer het materiaal bijvoorbeeld onder druk heeft gestaan. Bekende voorbeelden uit het dagelijks leven zijn oorspronkelijk vormeloze massa's zoals, meel en cement.
Na samenpersen in een handpalm kunnen deze stoffen al zodanig verstevigen dat zij als min of meer vast voorwerp op tafel kunnen worden gelegd.
Deze versteviging treedt bij bijna alle producten op, enerzijds door cohesie: het samenplakken van kleine deeltjes, maar ook door verandering van de pakking van deeltjes.
Kleine deeltjes kruipen tussen de grotere. Vliesvormige deeltjes oriënteren zich zo, dat de stapeling compacter wordt.
Versteviging is afhankelijk van het vochtgehalte, de stapeldichtheid en de temperatuur van het bulkgoed, maar de belangrijkste factoren zijn tijdsduur en consolidatiedruk.
Een ander voorbeeld van de twee eerstgenoemde invloeden ervaart een badgast aan het strand, die zowel in de duinen als tijdens het pootje-baden in zee ongeveer tot zijn enkels in het zand wegzakt. Tussen duin en zee echter treft hij tijdens eb een strook verhard zand aan waarover hij moeiteloos kan worden gewandeld. Wanneer een uitgestoken monster van dit verharde zand wordt verhit, verdampt het aanwezige water waardoor weer vormloos rul zand wordt verkregen. In dit geval heeft de temperatuurverhoging tot verzwakking geleid. Het omgekeerde vindt plaats bij materialen die bij verhoogde temperatuur chemische of fysische bindingen vormen op de onderlinge aanrakingspunten van de korrels. Literatuur[1] Palowitsch, E.R., en Goode, C.A.,'State of the Art of Bulk Materials Systems', Bulk Material Handling, Vol. 1, Univ. of Pittsburg, 1971 (Editor, Minor C. Hawk) [2] Rademacher, F.J.C., Haaker, G. en Kruyt, N.P.,'Silo's en Feeders', boek, Uitgave:'The Bulkoholics', 2e druk 1990.st StortgoedkarakteriseringMeting van bulkgoedeigenschappen in de industrieDe eigenschappen van een bulk solid zijn vooral afhankelijk van de technische toepassing. Een poeder gedraagt zich bijvoorbeeld anders tijdens opslag dan in een pneumatisch transportsysteem. InleidingDe eigenschappen van een poeder zijn een functie van de manier waarop met het poeder wordt omgegaan. Dit betekent dat de karakterisering van deeltjesverzamelingen altijd in relatie moet staan tot de bewerking ervan. Zo zal bij malen en tabletteren vooral worden opgelet op de eigenschappen die de maalbaarheid en de tabletteerbaarheid beïnvloeden. Bij transport en opslag van een poeder kunnen weer andere eigenschappen van belang zijn, zoals:
De uiteindelijke toepassing van het poeder kan weer eisen stellen aan heel andere eigenschappen, zoals het oplosgedrag, de uiteenvaltijd en de bevochtigbaarheid. Al deze eigenschappen dienen te worden gemeten, waarbij voor iedere eigenschap soms diverse meetmethoden beschikbaar zijn. De hoeveelheid eigenschappen van stortgoed, het nog grotere aantal meetmethoden en de talloze technieken die stortgoed kan ondergaan, hebben geleid tot diverse pogingen om het vakgebied van de stortgoedtechnologen op overzichtelijke wijze in kaart te brengen. IndelingenEen van de indelingen is in de 70'er jaren door de Werkgroep Stortgoedtechnologie voorgesteld, gebaseerd op de groepen van technieken zoals die zich in de praktijk voordoen:
Vanuit het oogpunt van deeltjestechnologie is een ander onderscheid te maken, en wel tussen de volgende natuurkundige disciplines:
De bestudering van alleen de mechanica van deeltjes, bijvoorbeeld bij opslag in een silo, zou voorbij gaan aan andere aspecten die het gedrag van de deeltjes beïnvloeden. In een silo kunnen deeltjes namelijk aan elkaar gaan plakken (oppervlak-fysica) of ook breken door de optredende drukken (vaste stoffysica). Verder zijn er altijd interacties met de omringende lucht die krachten op de deeltjes uitoefenen (twee-fasenstroming). Bij een indeling op basis van natuurkundige disciplines is het dus zaak om de karakterisering zodanig uit te voeren dat in ieder geval de belangrijkste discipline wordt belicht en de betekenis van de andere disciplines wordt ingeschat. Soorten loopgedragStortgoed kan op basis van de stromingseigenschappen ofwel het loopgedrag in grote lijnen in drie groepen worden ingedeeld:
ad.1. Vrijstromend stortgoed bestaat uit deeltjes die niet aan elkaar plakken. Deze deeltjesverzamelingen leveren in de praktijk over het algemeen geen problemen op. De deeltjesgrootte is meestal groter dan 100 μ (0,1 mm). Een voorbeeld is grof zand. ad.2. Cohesief stortgoed kenmerkt zich door de aantrekkingskrachten die tussen de deeltjes onderling optreden. Deze 'interparticle force' met name de Vanderwaalskrachten, geven aanleidingen tot plakgedrag. Bij droge stoffen treedt dit verschijnsel vooral op bij kleine deeltjes (30-100 μ). Bij grotere deeltjes kan vocht plakgedrag veroorzaken. ad.3. Beluchtbare poeders (aeratable powders) sluiten gemakkelijk lucht in en laten die soms moeilijk weer los. Als deze poeders in beweging zijn, kunnen ze zich gedragen als een vloeistof. In rust zijn ze meestal cohesief. De deeltjesgrootte is meestal kleiner dan 30 μ. Oorzaak van verschillen in loopgedragHet onderscheid tussen vrijstromende, cohesieve en beluchtbare poeders blijkt dus samen te hangen met de deeltjesgrootte. In feite zijn bij de karakterisering van poeders twee grootheden kenmerkend:
1. PorositeitHet blijkt dat de porositeit toeneemt bij afnemende deeltjesgrootte. De oorzaak hiervan is dat kleine deeltjes elkaar kunnen aantrekken (plakken) en daardoor 'gewelven' of 'agglomeraten'
vormen, waardoor ijle pakking ontstaat.
Porositeit afhankelijk van bewegingssnelheidDe porositeit van het stortgoed is afhankelijk van de bewerking die het ondergaat.
Bij tabletteren, briketteren, walsen en granuleren bevindt het stortgoed zich in een gecompacteerde staat met een porositeit die kleiner is dan 0.35.
Het mag duidelijk zijn dat de karakterisering van een poeder betrekking moet hebben op de staat van de deeltjes in het proces. 2. DeeltjesgrootteEr zijn veel meetmethoden om een deeltjesgrootte en een deeltjesgrootteverdeling te meten (tabel 1). Voor deeltjes groter dan circa 10 μ, zijn zeven en laserdiffractie de meest toegepaste methoden. De uitkomsten van een meting zijn afhankelijk van de toegepaste methode. Elke methode interpreteert het begrip 'diameter' namelijk op andere wijze. Het is daarom van belang om de diameter te definieren zoals past bij het proces waarin de deeltjes zich bevinden. In een verzameling hebben de deeltjes meestal niet allemaal dezelfde grootte. De spreiding van de deeltjes- grootte wordt weergegeven in een deeltjesgrootteverdeling. Enkele bekende deeltjesgrootteverdelingen zijn de log-normale verdeling, de Rosin Ramler Sperling (RRS) verdeling en de exponentiele verdeling. 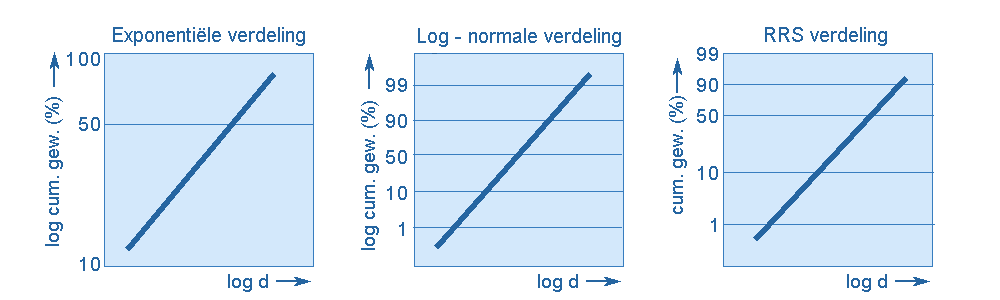
Door de verdelingen logaritmisch uit te zetten, ontstaat een rechte lijn. Het voordeel van het weergeven van totale verdelingen is dat de afwijkingen in het proces snel en gemakkelijk kunnen worden gedetecteerd. In granulatieprocessen zal veelal de log-normale verdeling worden gehanteerd; bij malen een RRS-verdeling. DeeltjesvormOm de vorm van de deeltjes te karakteriseren, zijn nogal wat vormfactoren bedacht. Met image-analysis kan onder andere de lengte/breedteverhouding worden gemeten, maar vaak is het handig om te kijken hoe de uitkomsten van twee verschillende technieken zich tot elkaar verhouden, bijvoorbeeld zeven en windziften.
3. DeeltjessterkteDe deeltjesgrootte(verdeling) is in de prakijk van transport en opslag ook afhankelijk van de deeltjessterkte. Immers, als een deeltje breekt of slijt ontstaan er nieuwe, kleinere deeltjes. Voor de meting van de sterkte van deeltjes is een groot aantal methoden beschikbaar. Het nadeel van de meting van enkel deeltjes is dat veel deeltjes moeten worden gemeten om een gemiddelde deeltjessterkte te vinden. De bepaling is tijdrovend. Snellere gaat het wanneer aan een verzameling deeltjes wordt gemeten (zoals dat bijvoorbeeld in de mengvoederindustrie gebeurt). Het nadeel daarvan is dat de spreiding in eigenschappen van individuele deeltjes onbekend blijft. 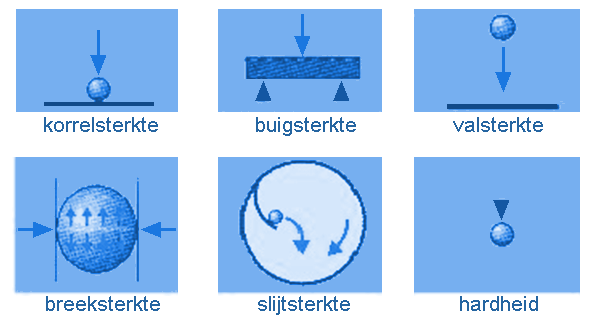
Verwarrend is dat bij sommige meetmethoden niet de sterkte of trekspanning wordt gemeten, maar de slijtsterkte (friability). Dit is de hoeveelheid materiaal die na een aantal keren botsen of vallen van het oorspronkelijke deeltje is verdwenen. Een essentiële factor bij de bepaling van de sterkte is de deformatiesnelheid. Diverse materialen (zoals kunststoffen) blijken sterker te zijn naarmate de deformatiesnelheid groter is. Dit betekent dat de sterkte moet worden gemeten bij de deformatiesnelheid die past bij het proces waarin de deeltjes zich bevinden. AttritieAttritie is het ongewenst breken van deeltjes. hierbij treden twee verschijnselen op: fragmentatie en abrasie. Bij fragmentatie breken de deeltjes in twee of meer brokken, bij abrasie breken of slijten de hoekjes en randjes van de deeltjes. Het optreden van attritie wordt zichtbaar in de deeltjesgrootteverdeling, het stortgewicht en het specifiek oppervlak van een poeder of granulaat. Het verschijnsel kan worden gemeten met veel technieken. Het verdient aanbeveling om de techniek te kiezen die aansluit bij de krachten en deformatiesnelheden, die de deeltjes in het proces ondervinden. In principe zijn er twee soorten testmethoden: impact- en compressietechnieken. Bij impacttechnieken wordt de breuk door botsing veroorzaakt. Bij compressie -of shear-technieken treedt breuk op door druk of afschuiven. De slijtvastheid van een granulaat wordt meestal vastgesteld aan de hand van de hoeveelheid afgebroken materiaal die bij een proef overblijft ten opzichte van de oorspronkelijke hoeveelheid materiaal. Zoals te verwachten is, bestaat een relatie tussen de slijtvastheid of friability enerzijds en de sterkte anderzijds. Overigens speelt de vorm van de deeltjes een essentiele rol. Ronde deeltjes geven minder slijtage of attritie dan niet-ronde deeltjes. 4. DeeltjesdichtheidBehalve de deeltjesgrootte is ook de deeltjesdichtheid van belang. Zwaardere deeltjes hebben minder last van cohesieve krachten. De deeltjesdichtheid (solid density, rho_s) staat via de porositeit (e) in verhouding tot de bulkdichtheid (rho_B, ook: stortgewicht, stortdichtheid, bulk density). De bulkdichtheid van een verzameling deeltjes is eenvoudig te bepalen: het is gewicht van een bepaalde hoeveelheid gedeeld door het ingenomen totaalvolume. Als we te maken hebben met poreuze granules, is er sprake van twee soorten porositeit: de bedporositeit (e_bed) en de of deeltjesporositeit (granuleporositeit). Voor gewone stapelingen geldt een bedporositeit van e_bed ongeveer 0.4. Als de granuleporositeit ook ongeveer zo'n waarde heeft, leidt dit tot een erg laag stortgewicht. Bulkdichtheid, Hausner RatioDe bekendste methode voor de meting van het stortgewicht is die waarbij in een maatcilinder het gewicht van een (standaard)volume wordt gemeten. Het bezwaar is dat de cilinder nogal nauw is en soms moeilijk te vullen (bijvoorbeeld met vezelig materiaal). Bovendien blijkt het stortgewicht nogal eens een functie van de vulwijze. Daarom zijn er methoden ontwikkeld waarbij een vaatje wordt gevuld op een standaard manier. Met dezelfde methode meet men ook de bulkdichtheid na kloppen, de 'tap density' (rho_t). Hiertoe wordt de maatcilinder 1250 maal gedefinieerd getikt, waarna de stortdichtheid wordt gemeten. Door de tap density door het stortgewicht te delen, ontstaat de Hausner Ratio. Deze verhouding kan worden gebruikt voor de indeling van poeders, waarbij een hogere waarde van de Hausner Ratio wordt gekoppeld aan slechter stroomgedrag (zie tabel). Het resultaat levert geen harde feiten, er is een vrij groot gebied dat als overgangsgebied wordt aangemerkt. De uitkomsten zijn sterk afhankelijk van de manier waarop zij bepaald zijn. Er moet dus altijd op worden gegeven hoe dit is gedaan.
Bepaling deeltjesdichtheidVoor het bepalen van de deeltjesdichtheid (solid density, rho_s) zijn diverse methoden beschikbaar, waarvan de Beckmann Air Comparison pyknometer en de gewone kwikpyknometer de bekendste zijn.
Meting stromingsgedragMeting van de mechanische eigenschappen (loopeigenschappen)BewegingssnelheidDe stromingseigenschappen van poeders zijn ahfhankelijk van de situatie waarin ze zich bevinden. Bij opslag en in de meeste transportapparatuur blijft de bewegingsnelheid van de deeltjes onderling laag. Bij deze bewegingen zal de wrijving tussen de deeltjes een belangrijke rol spelen. De stroming vindt plaats door het bezwijken van het bulkgoed. De mate waarin en het gemak waarmee dit gebeurt, noemen we het loopgedrag ofwel flowability. De schuifspanning is in deze situatie een functie van de normaalspanning, niet van de snelheid. Bij hogere snelheden vindt hoofdzakelijk botsing van deeltjes plaats en kunnen we spreken van een suspensiestroming (in lucht). De schuifspanning is hier een functie van de snelheid, niet van de normaalspanning. Hieronder wordt gesproken over de karakterisering van bulkgoed in lage snelheidssystemen. Afschuiftesters (shear cells)Voor het meten van stromingseigenschappen zijn diverse types afschuiftesters. Enerzijds zijn er testers waarmee fundamentele kennis over het gedrag van bulkgoed kan worden vergroot. Dit zijn zeer gespecialiseerde afschuiftesters, bijvoorbeeld de True Biaxial Shear Tester of de triaxiaal tester, met (zeer) bewerkelijke en soms gecompliceerde procedures. Anderzijds zijn er testers ontwikkeld om de loopeigenschappen te bepalen voor praktische toepassingen, bijvoorbeeld voor het ontwerpen van silo's. In onderstaande tabel worden een aantal testers genoemd die voor industriële toepassing worden gebruikt, hoewel de triaxiaaltester daar eigenlijk al buiten valt.
1) Standard Shear Testing Technique, Inst. of Chem. Engrs. 1989 Meting bezwijklijnDe bezwijklijn (yield locus) geeft informatie over de inwendige wrijving en samenhang van het product bij een zekere (silo)druk.
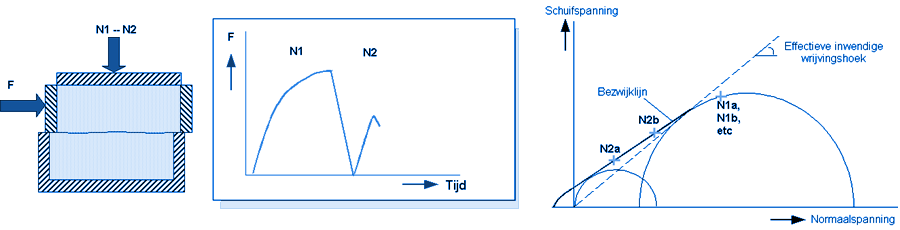
Bij de meting wordt op het monster een bepaalde belasting aangebracht en een horizontale verplaatsing opgelegd, waarbij de kracht wordt gemeten. De gemeten tau/sigma-verhouding bepaalt een punt van de bezwijklijn. Het afschuifvlak wordt gevormd in het product, daardoor is de verwerking anders dan bij de wandwrijving, waar het afschuifvlak opgelegd wordt door het wandmateriaal. ResultatenEen voorbeeld van de gegevens die gemeten worden bij het bepalen van bezwijklijnen (yield loci) zijn weergegeven in de onderstaande tabel. 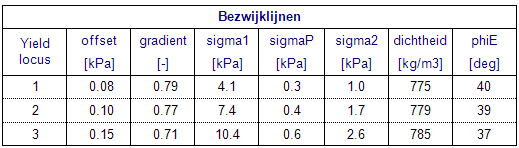
Een bezwijklijn geldt voor één toestand, met zekere condities (vochtgehalte, temperatuur, etc) en gekenmerkt door één drukniveau en daarmee corresponderende bulkdichtheid (rho). Vanuit de meetpunten wordt de bezwijklijn geconstrueerd. Er wordt aangenomen dat deze, in het gebied dat van belang is, benaderd kan worden door een rechte lijn (tau = gradiënt*sigma + offset). De waarde sigmaP (eigensterkte) geeft een indicatie van de cohesie bij het drukniveau sigma1 (vergelijkbaar met de verticale druk in een silo). Sigma1 is de grootste hoofdspanning, sigma2 de kleinste hoofdspanning. Verder wordt de inwendige wrijving (phiE) gevonden. Het stroomgedrag van verschillende producten kan vergeleken worden op basis van een bezwijklijn. Daarbij geld dat hoe groter de verhouding sigmaP/sigma1 is,
des te slechter de stroombaarheid van het product zal zijn. Meting tijdsconsolidatieWanneer een product enige tijd in de silo stilstaat treedt versteviging op. Hoe langer een product stilstaat, des te meer het verstevigt.
De versteviging kan leiden tot verergering van brugvorming of ratholing.
.png)
WandwrijvingsmetingBij het ontwerp van opslag- en transport-installaties speelt de wrijving van het stortgoed op de wand van de apparatuur een belangrijke rol. De eenvoudigste methode om deze wandwrijving te bepalen, is door een hoeveelheid stortgoed op een plaat van het wandmateriaal te plaatsen en vervolgens te meten onder welke hoek het stortgoed van de plaat afschuift. Een beter resultaat verkrijgt men met behulp van een shearcel. Hierbij schuift men een plaatje wandmateriaal van het poeder af, waarbij de kracht die hiervoor nodig is nauwkeurig wordt gemeten. 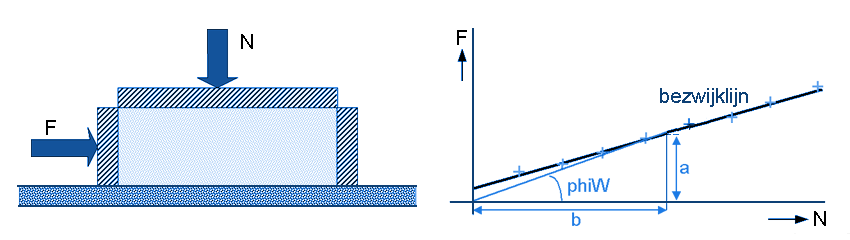
Veelal houdt de wandwrijving verband met het loopgedrag van het stortgoed. Vooral de vorm van de deeltjes blijkt belangrijk te zijn.
Langwerpige deeltjes glijden meer dan dat ze rollen, waardoor ze aanleiding geven tot een hoger wandwrijving dan bolvormige deeltjes.
Jenike shear cellIn de praktijk blijkt de Jenike shearcell meestal het best bruikbaarVaak denkt men bij product-eigenschappen vooral aan de chemische samenstelling. Deze samenstelling is voor de functionaliteit inderdaad van het grootste belang. Bij de handling van stortgoed spelen echter andere eigenschappen de hoofdrol. Het gaat dan om de zogenoemde mechanische eigenschappen die bepalen of en hoe het stortgoed stroomt. In de afgelopen decennia zijn diverse instrumenten ontwikkeld om deze eigenschappen te meten, maar nog steeds is men op zoek naar testers waarmee redelijk eenvoudig zeer nauwkeurig of zeer eenvoudig redelijk nauwkeurig kan worden gemeten. Het ei van Columbus is nog niet gevonden. Metingen stromingseigenschappenDe Jenike shear cell, ook Jenike shear tester genoemd, is een oudgediende onder de testers. Hij heeft zijn wortels in de grond-mechanica en werd in de jaren 60 gelijktijdig met silo-theorieen ontwikkeld door A.W. Jenike.
Met deze shear cell worden punten van een bezwijklijn gemeten. De meting geschiedt nadat een zogenaamde 'steady state' is bereikt (een fase van continu bezwijken).
Deze situatie is vergelijkbaar met stroming in een silo, zodat de gevonden waarden te relateren zijn aan een bepaalde plek (drukniveau) in de silo.
Omdat het drukniveau in een silo theoretisch goed te bepalen is (via o.a. de Janssen-theorie), hebben de resultaten van de metingen een goede aansluiting op theorie en praktijk.
.jpg)
Meetprocedure
Het grootste nadeel van de shear cell is dat voor elke bezwijklijn (yield locus) minstens vier geldige meetpunten nodig zijn.
Zes of meer meetpunten geven meer zekerheid, vooral bij moeilijke producten.
Bij bulkgoederen met veel cohesie is het meetgebied vrij klein, waardoor metingen snel buiten het geldige gebied vallen.

Alternatieve testersSinds het bestaan van de tester wordt daarom gezocht naar alternatieven, waarbij men zich richt op drie meettechnieken: fundamentele testers, shearcells en snelle testers. Fundamentele testersDe fundamentele testers moeten meer inzicht geven in het complete bezwijkgedrag van stortgoed.
De apparatuur hiervoor is in ontwikkeling, maar nog niet commercieel inzetbaar of verkrijgbaar.
In deze categorie valt bijvoorbeeld de 'true biaxial tester'.
Met deze tester kunnen driedimensionaal spanningen of vervormingen worden opgelegd dan wel gemeten.
Shear cellsIn de tweede plaats probeert men nieuwe shear cell testers te ontwikkelen waarmee in principe
dezelfde eigenschappen kunnen worden gemeten als met de Jenike shear cell. Zie ook afschuiftesters hierboven.
De inspanningen richten zich met name op de ontwikkeling van een meetprocedure die eenvoudiger is dan die van de Jenike shear cell.
De meetresultaten dienen uiteraard een minstens gelijke nauwkeurigheid te hebben.
Een voorbeeld is de constant-volume-tester, waarmee in een meting een complete bezwijklijn is te bepalen.
Snelle testers
De derde meettechniek betreft de ontwikkeling van snelle testers. Bij deze testers ligt de nadruk op een eenvoudige procedure.
Te noemen zijn onder meer de doordrukproef, de cake-tester en de Johanson indicizer.
Het betreft hier apparatuur waarmee snel een indruk van het bezwijkgedrag kan worden verkregen,
zonder dat direct duidelijk is wat er precies wordt gemeten.
Verwerking resultaten
In de meeste gevallen gaat de voorkeur toch uit naar de Jenike shear cell, te meer daar met deze tester ook relatief eenvoudig de
wandwrijving en de tijdsinvloed zijn te meten.
De nadelen van de tijdrovende procedure en de vereiste kennis en ervaring om het apparaat te bedienen, blijven echter bestaan.
Een aantal aanpassingen kunnen echter de bediening vergemakkelijken en de procedure versnellen.
Verder is veel tijd te winnen in de verwerking van de meetgegevens tot bruikbare grootheden.
Met behulp van een computerprogramma kan dit werk snel en flexibel worden uitgevoerd.
De gemeten krachten worden omgerekend naar spanningen, waarbij automatisch met de afmetingen en gewichten van de shear cell-onderdelen rekening wordt gehouden.
Referenties
Wandwrijving in de bulktechnologieWaar treedt het op, en hoe kunnen we het meten
Introductie Wandwrijving bij silo-opslagBij de opslag in silo's heeft de wandwrijving een driedelige invloed:
Bij 3) Wandwrijving en slijtageHet relatieve slijtpatroon (w) van twee massastroomsilo’s, de één met een vlak symmetrisch stromingsprofiel, de ander met een axiaal-symmetrisch stromingsprofiel, is hieronder aangegeven. (Zoals gebruikelijk bij silo’s is de variabele die normaal verticaal wordt uitgezet hier horizontaal uitgezet, zodat de silo rechtop kan blijven staan.) 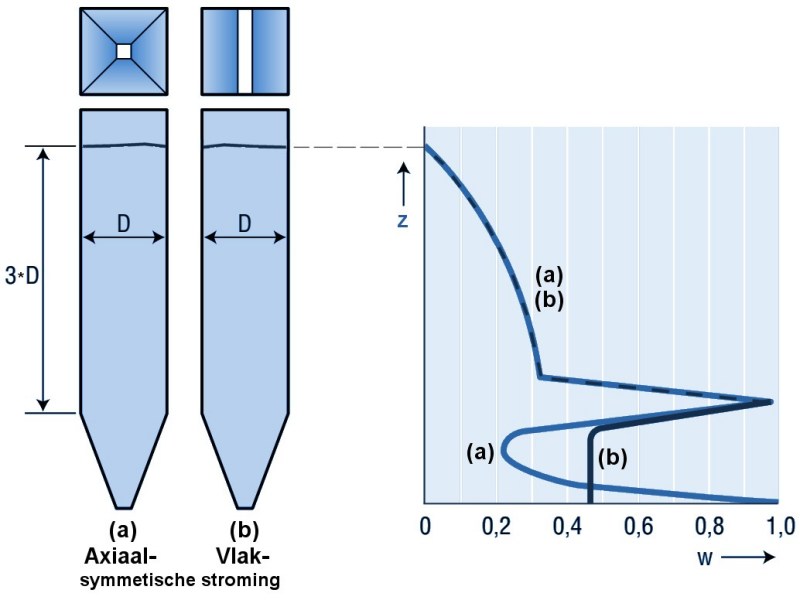
Bij een hogere waarde van w is de slijtage groter. We zien een piek voor beide stromingstypes bij de overgang van cilinder naar conus. Dit komt doordat daar ter plaatse fors grotere wanddrukken optreden. Bij de axiaalsymmetrische trechter treedt in sommige gevallen nog een piek in slijtage op vlak boven de uitstroomopening omdat hier de schuifsnelheid hoger is. Maar omdat de wanddrukken daar laag zijn, is de piek niet altijd aanwezig. Wandwrijving bij mechanisch transport
Bij mechanisch transport hebben we ook te maken met wandwrijving en inwendige wrijving.
Wandwrijving treedt op aan de buitenkant van het bulkgoed, daar waar bulkgoed de wand raakt.
Het oppervlak is daarbij goed gedefinieerd door het transportwerktuig.
Men onderscheidt statische wandwrijving, wanneer bulkgoed in beweging moet komen, en dynamische wandwrijving,
wanneer het eenmaal aan het glijden is. De wandwrijving is niet of nauwelijks snelheidsafhankelijk.
Wandwrijving betekent slijtage aan apparatuur. Bij de werktuigen waarbij het bulkgoed niet beweegt ten opzichte van de transporteur, zoals bij bandtransporteurs en bekerelevatoren treedt de meeste slijtage op bij de invoer/toevoer en uitvoer/afworp van de transporteur. Slijtage is daardoor plaatselijk en daarom zijn slijtdelen op deze plaatsen gebruikelijk. Bij andere werktuigen, zoals bij schroeftransport, buistransport of kettingtransporteurs (Redlers) treedt slijtage op over het hele oppervlak waar stortgoed in glijdend contact is met de transporteur. Slijtage blijft meestal beperkt, omdat de snelheden laag blijven, zeker als het werktuig ruim ontworpen is voor de gewenste capaciteit. Bij zeer abrasieve stortgoederen zal echter ook de gehele transporteur van een beschermende laag moeten worden voorzien. Wandwrijving bij pneumatisch transport.jpg)
(bron: hammertek.com)
Bij pneumatisch transport is het drukverlies in het leidingsysteem een belangrijke ontwerpgrootheid.
Hierbij speelt de wandwrijving een rol bij vanwege de wandruwheid.
Verder zal ten gevolge van de remmende krachten op de deeltjes bij het glijden langs en het botsen met de wand
zowel een bochtverlies als een stationair drukverlies in de leiding optreden.
Wandwrijving bij andere bewerkingenBehalve in bovengenoemde voorbeelden zijn ook in het gebied der bewerkingen vele situaties te herkennen waar wandwrijving een rol speelt. Hierbij valt bijvoorbeeld te denken aan de invloed van wandwrijving bij het persen van tabletten. Kort gezegd zal overal waar een stortgoed in aanraking komt met een ander materiaal wrijving een rol spelen. Factoren die de wandwrijving bepalenDe wandwrijving zoals deze zich in een bepaalde situatie voordoet is afhankelijk van drie groepen parameters:
Wanneer men de wandwrijving wil weten, is het belangrijk te meten aan een representatief stortgoedmonster. Soms moet dat een monster zijn waarbij al breuk is opgetreden. Of moet het (een overmaat van) een bepaalde fractie zijn, omdat die het gedrag bepaald. De testplaat moet vanzelfsprekend hetzelfde zijn als het toegepaste materiaal. Maar ook hier kan slijtage of bijvoorbeeld versmeren van vetten uit het stortgoed van invloed zijn. Verder dient de test de praktijksituatie zo goed mogelijk na te bootsen qua belasting en snelheden. Meten van de wandwrijving
Hoewel er in de loop der tijden diverse methoden zijn ontwikkeld, bestaat er eigenlijk maar één standaardmethode
voor het meten van de wandwrijving, de zogenaamde Jenike sheartest. Hierbij wordt het product opgesloten
in een starre stalen of messing ring (diameter ca 100mm, hoogte ca 16mm), en voorzien van een bovendeksel
waarmee het monster via een juk met gewichten verticaal wordt belast (N). 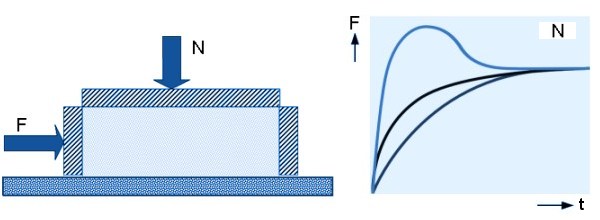
Hierboven staat een schematische weergave van de shearcell en drie mogelijke profielen van de gemeten schuifkracht.
Bij de twee laagste lijnen neemt de wrijving neemt langzaam en iets sneller toe tot het de eindwaarde bereikt.
Bij de bovenste curve is er sprake van een hogere statische wrijving. Pas nadat de piek in afschuifkracht is bereikt begint het monster te bewegen.
In dit geval is dus sprake van een duidelijk verschil in de statische en de dynamische wrijving, waarmee rekening moet worden gehouden bij later gebruik van de wrijvingswaarden.
Meten van de wandwrijving voor damwandsilo’s
Wat de invloed is van een geprofileerde wand, is onderzocht aan de Universiteit Twente met behulp van zowel een modelsilo als met een schuiftest.
Bij de modelsilo is de resulterende wandwrijving berekend op basis van de belasting die door de wand is opgenomen,
en dus niet wordt teruggevonden als gewicht op de weegschaal waar de inhoud op steunde.
Bij het leegstromen van dit model is een opname gemaakt, waarop te zien is dat het stortgoed in het profiel stil staat.
Wandwrijvingsmeting van stortgoedMeting toch niet zo simpel als het lijktDe wandwrijving tussen een stortgoed en de wand speelt een belangrijke rol in de stortgoedtechnologie. De belasting op silowanden en bodem, en daarmee de benodigde wandsterkte, zijn sterk afhankelijk van de optredende wandwrijving, vooral bij hoge, slanke silo’s. Het stromingspatroon dat optreedt in een silo wordt hoofdzakelijk bepaald door de wandwrijving. Daarmee heeft het invloed op het gebruik van de silo, en ook weer op de belastingen. Verder is in vele processen de wandwrijving een belangrijke factor voor het benodigde mechanische vermogen voor een proces. In vergelijking met grootheden als de inwendige wrijving en eigensterkte (cohesie) van een bulkgoed, is de wandwrijving eenduidig en de meting tamelijk eenvoudig. Dit in tegenstelling tot het meten van de bezwijklijn, waaruit inwendige wrijving en in tweede instantie eigensterkte worden afgeleid. Deze meting moet worden uitgevoerd aan een zorgvuldig geprepareerd monster, zodat de bulkdichtheid de juiste waarde heeft, en het gevormde afschuifvlak de juiste vorm. Daardoor is de meetprocedure bewerkelijk en vergt de nodige vaardigheid. Het meten van de wandwrijving is in principe veel eenvoudiger: een monster van het stortgoed wordt over een plaat wandmateriaal geschoven, waarbij de kracht wordt gemeten. Gebleken is echter dat het zo eenvoudig niet is. In een gezamenlijk project van de Europese Werkgroep uitgevoerd rondom de eeuwwisseling, zijn metingen van de wandwrijving verricht door 13 laboratoria wereldwijd. De resultaten bewijzen dat deze metingen zorgvuldig dienen te worden uitgevoerd, onder beschouwing van de juiste condities, en rekening houdend met (soms ruime) marges. 
Wandwrijving
In het verleden is wandwrijving veelal als een tamelijk simpele grootheid opgevat. De wandwrijvingscoëfficient voor een bepaalde stortgoed- / wandcombinatie werd meestal als constante beschouwd, die met eenvoudige sleepproeven konden worden bepaald. Nieuwere inzichten hebben echter aangetoond dat de wandwrijvingscoëfficient van een zekere stortgoed-/wandcombinatie niet een unieke en constante waarde is, maar afhangt van de optredende omstandigheden qua snelheid, druk, temperatuur etc. Dit impliceert dat metingen die het wrijvingsgedrag in een of ander proces moeten voorspellen, dan ook onder vergelijkbare procescondities moeten worden gemeten.
Studie meting wandwrijvingWellicht vanwege de eenvoud van de test en het gemak van uitvoeren, is er in de literatuur niet veel aandacht voor interpretatie en vergelijking van resultaten. Een uitzondering hierop is een studie opgezet in 1994 door de WPMPS (Working Party on the Mechanics of Particulate Solids), waarin de diverse testmethoden zijn onderzocht op hun betrouwbaarheid en toepassingsgebied. Bij dit project zijn resultaten van 13 ervaren stortgoedlaboratoria vergeleken. Testprocedure
Als eerste stap in de WPMPS-studie werd gekozen voor de Jenike tester , die algemeen wordt beschouwd als de standaardtester voor het ontwerpen van silo's. De Jenike sheartester is een translerende tester, waarin het te testen stortgoed is opgesloten in een stijve metalen ring en in verticale richting wordt belast via een bovenplaat (deksel) waarop een juk met gewichten rust. Het belaste stortgoedmonster wordt vervolgens afgeschoven over een testplaat van het te wandmateriaal, waarbij de benodigde afschuifkracht wordt gemeten. Een schematische voorstelling van de tester is gegeven in Afb. 1.
Bovenstaande SSTT-testprocedure werd zo nauwkeurig mogelijk aangehouden. Echter met een uitbreiding van de laatste stap: er is ook met toenemende verticale belasting gemeten. In overeenstemming met de SSTT werden 6 waarden voor de verticale druk in het bereik 1 tot 15 kN/m² gekozen. Stortgoed/wand combinaties
Metingen zijn verricht met drie stortgoederen en drie testplaatjes, zodat 9 combinaties zijn gemeten. Alle stortgoedmonsters zijn vanaf één adres in gesloten vaatjes verzonden, terwijl ook de testplaatjes, steeds afkomstig uit één grotere moederplaat, vanuit hetzelfde adres naar de deelnemers zijn gestuurd. Als stortgoed werd gebruikt: fijn zand; heavy soda ash (natrium carbonaat) en BCR limestone. Het laatste materiaal is het EU referentie-materiaal voor sheartests.
Meetresultaten
Voor het onderzoek zijn alle metingen zijn tweemaal uitgevoerd, elke meetserie met een vers stortgoedmonster. De piek in de schuifkracht die bij sommige stortgoed/wand combinaties optreedt, en de statische wandwrijving weergeeft, is niet meegenomen. In de resultaten is alleen rekening gehouden met de eindwaarden van de schuifkracht. Dit is de dynamische wandwrijving.
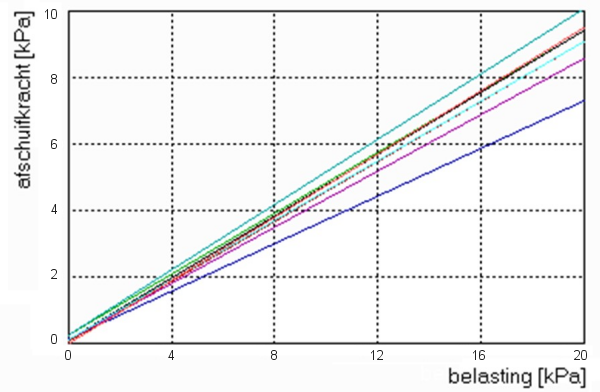
Een overzicht van de gemeten spreiding in de resultaten van de drie stortgoederen en drie soorten wandmateriaal is gegeven in onderstaande tabel.
Praktische bruikbaarheid voor silo-ontwerp
Gezien de grote verschillen in de gemeten wandwrijving, is het zinnig om te kijken naar de bruikbaarheid van dergelijke resultaten in de praktijk. Een van de belangrijkste toepassingen is het ontwerpen van silo’s. Bij het geometrisch ontwerp van hoppers wordt voor ronde trechters een veiligheidsmarge van 2 tot 4 graden aangehouden voor de benodigde hellingshoek. Op basis van de grenslijnen voor massastroming (Jenike) kan worden afgeleid dat veiligheidsmarge van 4 graden overeenkomt met een verschil in wrijvingshoek van ca. 3 graden. Hierbij is alleen te laag gemeten wandwrijving van belang, als de wandwrijving in de praktijk lager uitvalt, is er geen probleem.
Praktische bruikbaarheid voor drukberekeningIn een aantal silocodes wordt aangeraden om wandbelastingen te berekenen op basis van gemeten wandwrijving, wanneer in de code geen waarde wordt vermeld. Dan dient men zich wel te realiseren dat de maximale waarde van de wandbelasting omgekeerd evenredig is met de waarde van de wandwrijvingscoëfficient. Dus zal een maximale afwijking in de gemeten wandwrijving ook leiden tot eenzelfde afwijking in de berekening van de silobelasting. Ondanks de veiligheidsmarges die in silocodes zijn ingebouwd, is het in deze gevallen verstandig om niet al te zeer op het randje te construeren. Discussie
In het studie van de WPMPS, Europese Werkgroep op het gebied der Bulktechnologie, zijn door 13 laboratoria wereldwijd wandwrijvingen gemeten met een Jenike sheartester aan 9 combinaties van bulkgoed en wand. Alle gebruikte wandplaten en bulkmaterialen werden vanuit één bron gedistribueerd over de deelnemers. Verder was de te volgen testprocedure uitgebreid voorgeschreven en besproken om eventuele fouten tengevolge van afwijkende interpretaties en/of testmethodes uit te sluiten.
ConclusieWanneer we kijken naar de (meest belangrijke) toepassing voor hopper ontwerp en berekening van wandbelastingen kunnen we concluderen:
De in dit project van de WPMPS gevonden resultaten tonen duidelijk aan dat wandwrijving een ingewikkelder fenomeen is dan dikwijls wordt aangenomen en zorgvuldig moet worden gemeten, rekening houdend met praktijksituatie en praktijkinvloeden. Literatuur[1] Haaker, G. (1999): Wall Friction Measurement on Bulk Solids: Results of Comparative Measurements on 9 Bulk-Solid/Wall Combinations from 13 Laboratories Using the Jenike Sheartester, Powder Handling & Processing, 11( 1), pp. 19-26. Stroming uit silo’s gaat niet vanzelfStromingstechnieken moeten de basis vormen van elk ontwerpIn de loop van de tijd werd de opslagsilo steeds geavanceerder. Dat bracht de nodige hoofdbrekens met zich mee. Opslaan vergt meer dan in een silo brengen en er op zijn tijd weer uithalen. Hieronder volgt een beschrijving van verschillende uitvoeringen van opslagsilo’s, problemen die kunnen optreden en eventuele oplossingen. Ontwikkeling bulkhandlingDe kunst van het opslaan van producten is al bijna zo oud als de mensheid zelf, omdat een groot gedeelte van de in het warme seizoen geoogste of verzamelde voedselvoorraad moest op de een of andere manier worden bewaard om de winter door te komen. Dit gebeurde aanvankelijk in gaten in de grond, of in een soort hutjes of grotten. Later volgde de manshoge aardewerk vaten waar het product, meestal een graansoort, van boven werd ingebracht en in een later stadium door dezelfde opening er weer naar behoefte kon worden uitgeschept. Een dergelijke graansilo wordt tot op heden soms nog gebruikt bij kleine landbouwgemeenschappen in Afrika. Er komen niet vaak problemen bij dit soort opslag voor: Het gaat om bekende producten in een simpel en betrouwbaar opslagsysteem. Bij de opslagsystemen zoals we die in onze geïndustrialiseerde wereld tegenkomen liggen de zaken wat ingewikkelder. Ze blijken soms zelfs de bottleneck in het productieproces. 
Silogeometrie
De meest toegepaste silo’s bestaan uit een cilindrisch bovendeel; rond, vierkant of rechthoekig,
en een trechtervormig uitloopgedeelte; een conus, of een door plaatdelen samengestelde vorm.
Het opslagproduct wordt met een pneumatisch of mechanisch transportsysteem van boven in de silo gebracht.
Aan de onderzijde van de silo kan de benodigde hoeveelheid weer worden onttrokken.
De stroming door de silo vindt door de zwaartekracht plaats. Soms geholpen door stromingsbevorderende hulpmiddelen.
Slanke silo’s
Wanneer de verhouding (H/D) groter is dan twee, spreken van slanke silo’s (slender silos).
In de praktijk hebben meeste slanke silo's een diameter van 2 tot 4 m, maar ook diameters van 10 m komen voor.
De opslagcapaciteit ligt in de range van 10 tot 300 kubieke meter.
Mammoetsilo's, platbodemsilo's
In tegenstelling tot dit type slanke cel of silo staan de zogenaamde platbodem- of mammoetsilo's (squat silos). De silo bestaat dan meestal alleen uit verticale wanden;
de trechter ontbreekt of is zeer vlak uitgevoerd. De hoogte/diameter verhouding van dit soort silo’s is meestal kleiner dan 1.
De cilinderdiameter kan wel 60 meter bedragen. Opslagcapaciteiten liggen tussen de 1000 en 100.000 kubieke meter.
Stromingspatronen
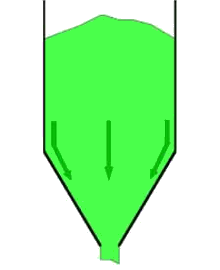
Bij het naar beneden stromen van een product in een silo zijn twee hoofdtypen stroming te onderscheiden: massastroming en kernstroming. MassastromingBij massastroming beweegt de hele productmassa mee op het moment dat er product aan de silo wordt onttrokken. Er is sprake van “First-in, First-out” (FiFo). Hoewel er kleine snelheidsverschillen kunnen optreden is er geen sprake van stilstaande zones. Doordat stroming over de gehele doorsnede van de silo plaatsvindt zijn de stroomsnelheden betrekkelijk laag en ontstaat een regelmatige stroming die goed regelbaar is. Dit type stroming wordt gekenmerkt door:
Nadelen van massastroming kunnen zijn dat in specifieke gevallen schokken kunnen ontstaan. Bij abrasieve producten zullen de silowanden meer slijten. Door de lage stroomsnelheden in een silo vormt dit echter doorgaans geen probleem. Met de theoriën van Jenike is voor verschillende trechtervormen te bepalen welk type stromingspatroon op zal treden. KernstromingBij kernstroming blijft het product aan de wand aanvankelijk in rust en vindt stroming plaats door een in het product zelf gevormde trechter of kanaal boven de uitstroomopening. Dit kanaal wordt van bovenaf vanuit de stilstaande gebieden bijgevuld. Hier is uiteraard geen sprake van first-in, first-out. De stroming is minder regelmatig door het soms schoksgewijs instorten van de dode zones. 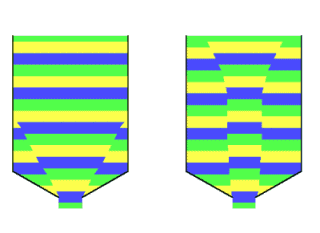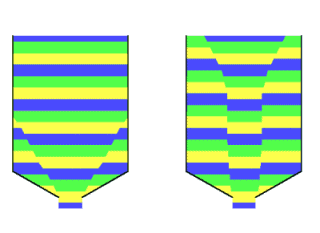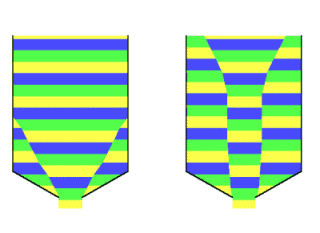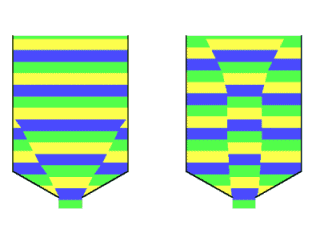
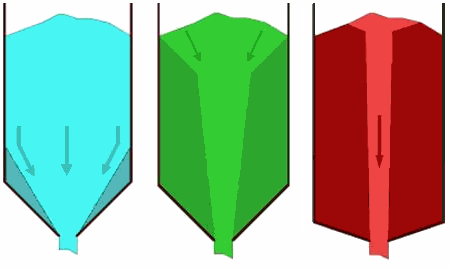
Bij kernstroming kunnen de volgende problemen ontstaan:
Kernstroming is daarom alleen toe te passen voor grove, vrijstromende producten, waarbij bederf of veroudering geen rol speelt. Welk type stroming in een silo zal optreden is afhankelijk van de inwendige wrijving van het product, de wrijving tussen product en silowand en de steilheid en geometrie van de uitstroomtrechter. Hoe steiler de trechter, des te groter de kans op massastroming. Met de theoriën van Jenike is voor verschillende trechtervormen te bepalen welk type stromingspatroon op zal treden. TrechtervormenDe trechterhoek waarbij nog massastroming optreedt is te berekenen voor een bepaalde trechtervorm als de inwendige wrijving en de wandwrijving bekend zijn. Qua trechtervorm zijn er twee hoofdgroepen:
Axiaalsymmetrische stromingBij ronde trechters (conussen), rechthoekige (piramidevormige) trechters treedt zogenaamde axiaalsymmetrische stroming (axisymmetric flow) op. Hierbij moet het product door een zich alzijdig (rond) of in twee richtingen (rechthoekig) vernauwende doorsnede stromen. 
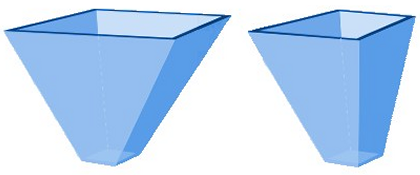
Vlaksymmetrische stromingBij een wigvormige trechter vindt vernauwing slechts in een richting plaats, dit wordt vlakke stroming (plain strain flow) genoemd. Het product ondervindt minder weerstand bij het uitstromen, wat erin resulteert dat massastroming al bij een minder steile hoek zal optreden. 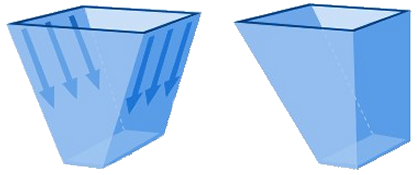
In de praktijk heeft massastroming meestal de voorkeur boven kernstroming, vooral vanwege het voordeel first-in, first-out. Een nadeel van massastroming is dat de inhoud langs de silowand glijdt, met slijtage als gevolg. Vanwege de lage snelheden in de silo, geeft dit in de praktijk alleen problemen bij zeer abrasieve producten (harde producten) of producten vervuild met harde deeltjes. Trechterhoek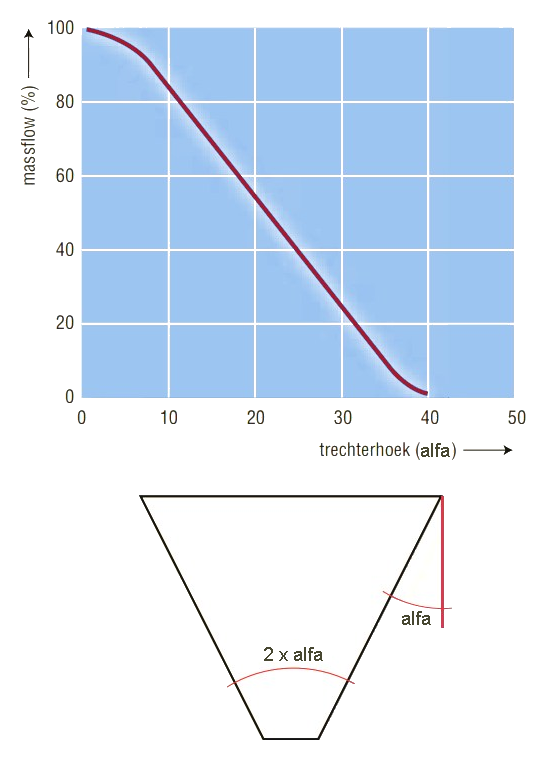
Verder verdient de benodigde hoogte van de trechter aandacht. Bij problemen kunnen tussenoplossingen de massastroming zo goed mogelijk benaderen zodat een minder hoge trechter volstaat.
De soms gehoorde opmerking dat altijd massastroming zal optreden bij een trechterhoek van 30 graden met de verticaal (60 graden met de horizontaal; ofwel een tophoek (ingesloten hoek) van 60 graden),
gaat helaas lang niet altijd op. Hieruit valt af te lezen dat voor axiaalsymmetrische stroming bij een conushoek van 30 graden met de verticaal slechts bij een kwart van de onderzochte combinaties massastroming zal optreden. Bij vlakke stroming schuift de curve acht à tien graden naar rechts (niet ingetekend), zodat in ongeveer de helft van de gevallen massastroming optreedt. StromingsproblemenBrugvormingBij het ontwerpen van een silo moet naast het type stroming, rekening gehouden worden met het mogelijk optreden van brugvorming of schachtvorming. Bij een silo met massastroming is de voornaamste storingsbron het optreden van min of meer stabiele bruggen die de stroming ontregelen of geheel doen stoppen. Bij grote stortgoeddeeltjes zal het om een mechanische verklemming van een aantal deeltjes boven de uitstroomopening gaan. Dit kan worden voorkomen door de uitstroomdiameter zeven tot negen maal groter te kiezen dan de grootste brokken product. 
bruggen.gif)
Bij poeders en bij producten met een aandeel kleine deeltjes treedt brugvorming op door cohesie.
Door de samenhang tussen een groot aantal deeltjes kan zich een stabiel gewelf vormen.
Dit kan optreden in de cilinder (het deel met verticale wanden), maar meestal vindt brugvorming in de trechter plaats.
Op basis van de producteigenschappen (stromingseigenschappen, loopeigenschappen) en de silotheorie kan een minimale grootte
van de uitstroomopening worden gekozen waarbij stabiele brugvorming niet zal optreden.
TijdsconsolidatieOok de opslagtijd speelt een rol. Brugvorming in de cilinderOm de inhoud van de silo van tijd tot tijd te laten stromen helpt echter niet tegen consolidatie in de cilinder (het verticale deel). Het product daar hoeft namelijk niet ten opzichte van elkaar te bewegen; het kan als één blok materiaal naar beneden zakken.Als de productversteviging groot is, en/of de silodiameter relatief klein, kan de brugsterkte zo groot worden dat de overspanning van een stabiele brug groter kan worden dan de silodiameter. Op dat moment kan een brug blijven staan in de cilinder. Meestal is dat op de overgang van cilinder naar trechter. Bij damwandsilo's (cellen gemaakt met horizontaal geplaatste damwandprofielen), of wanneer er zich een richel of rand in de cilinder bevindt, kan een brug steun vinden op een grotere hoogte van de overgang. Instorten van een dergelijke brug kan door de impact veel schade veroorzaken (de trechter kan in één klap onderuit geblazen worden). SchachtvormingBij kernstroming is het hoofdprobleem het optreden van een stabiel stroomkanaal dat kan leegstromen terwijl de rest van het product niet in beweging komt. Ook in dit geval kan op basis van producteigenschappen en theorie een minimale opening worden gekozen die deze stabiele schachtvorming vermijdt. Daarnaast moet uiteraard stabiele brugvorming in het optredende stroomkanaal worden voorkomen. Een deugdelijk ontwerp is maatwerk; het weegt de werkelijke eigenschappen van het product met de omstandigheden waaronder het wordt opgeslagen. Silo-ontwerp: MassastromingDoel: massastroming door zwaartekracht in een eenvoudige siloIn dit verhaal wordt ingegaan op de klassieke methode voor het ontwerpen van silo's, aan de hand van het meest voorkomende type silo, die bestaat uit een verticaal cilindrisch bovenstuk met daaronder een uitlooptrechter. Belangrijkste eis in het ontwerp is dat ongestoorde massastroming moet optreden. Siloontwerp is maatwerkHet ontwerpen van een silo heeft veel weg van het werk van een goede kleermaker.
Zoals de laatste moet weten wat de eisen en wensen zijn van de klant die zijn creatie zal dragen, zal ook de silo-ontwerper moeten uitgaan van de eisen van de gebruiker.
En waar de kleermaker nauwkeurig de maten van zijn cliënt moet opmeten, moet ook de silobouwer de eigenschappen weten (of meten) van het product dat zal worden opgeslagen.
Kortom, ook silobouw is veelal maatwerk. Bij massastroming zal al het product in de silo in beweging zijn en zullen er dus geen dode zones optreden. Verder geldt dat het product dat als eerste in de silo komt, er ook als eerste weer uitstroomt, het zogenaamde first in - first out principe (FiFo). Verder zal er weinig ontmenging in de silo optreden en bestaat er een regelmatige en goed regelbare uitstroming. Vanwege deze gunstige eigenschappen zal in veel gevallen voor massastroming worden gekozen. Zeker wanneer bederf, ongewenste vermenging of veroudering van het opslagproduct een rol spelen. StromingspatroonHet type stroming dat in een silo zal optreden, wordt bepaald door het gedrag van het stortgoed in de uitstroomtrechter. Wanneer het product in de gehele trechter langs de wand stroomt, zal dit ook in de rest van de silo gebeuren en spreken we over een zuivere massastroming. Stroomt het product in de trechter slechts ten dele of in het geheel niet langs de wanden maar meer in een intern stroomkanaal, dan zal dit ook voor de rest van de silo gelden. Hooguit kan er in dit geval hoger in de cilinder een lokale vorm van massastroming optreden, maar dieper in de silo zullen stilstaande of slecht stromende gebieden ontstaan. Met alle nadelen van dien. Het stromingsgedrag van het product in de trechter wordt in hoofdzaak bepaald door de steilheid van de trechter en de wrijving tussen product en wandmateriaal. In de bepalingen van het stromingpatroon wordt de trechterhoek met de verticaal (alfa) gebruikt. De wandwrijving wordt uitgedrukt als de hoek (phiW) tussen de x-as en de wandbezwijklijn, of als coëfficiënt (mu = tan(phiW) ). De inwendige wrijving van het stortgoed speelt een ondergeschikte rol. Massastroming
In de klassieke silotheorie zoals ontwikkeld door onder andere A.W. Jenike, is afgeleid voor welke combinaties van alfa en phiW
massastroming zal optreden, voor verschillende waarden van de inwendige wrijving.
In onderstaande diagrammen is dit aangegeven voor twee soorten stroming: axiaal-symmetrische stroming en vlakke stroming.
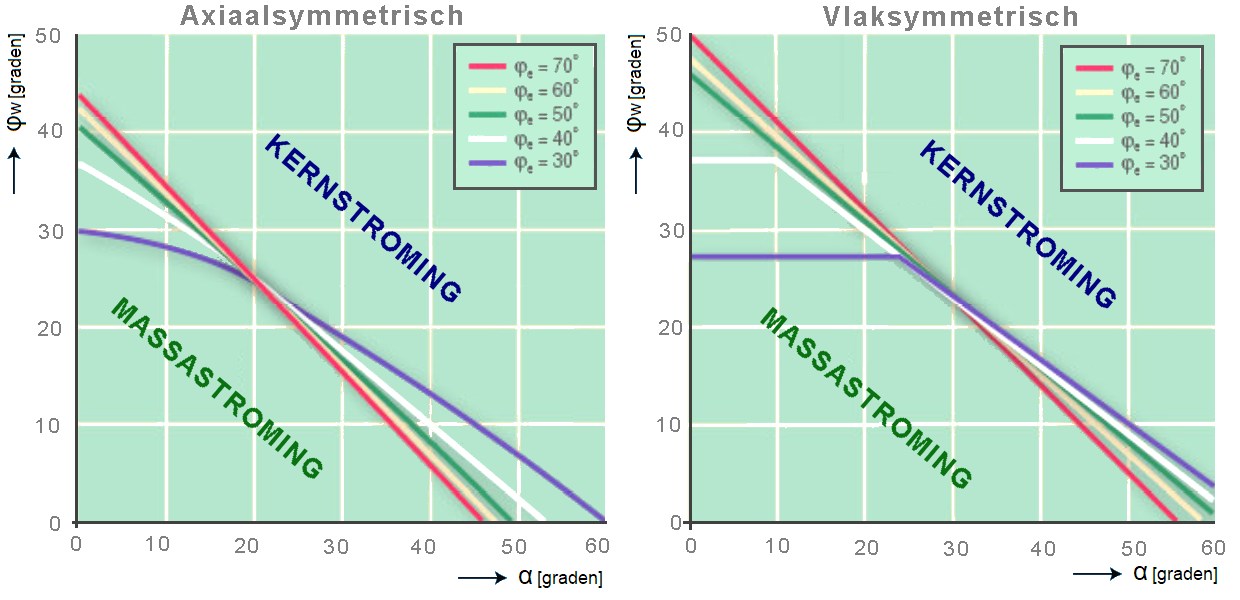
In de figuur is te zien dat ook de inwendige wrijvingshoek van het bulkgoed (aangegeven met phiE) een kleine invloed heeft. Wanneer dus de wandwrijvingshoek phiW tussen het bulkgoed en het beoogde wandmateriaal bekend is (deze zal gemeten moeten worden) kan de trechterhoek alfa zo worden gekozen dat massastroming zal op treden. Dit geldt zowel voor vrij stromende als voor cohesieve materialen. In het geval van axiaalsymmetrische stroming wordt in de praktijk meestal een conushoek gekozen die ca 3° steiler is dan de gevonden grenswaarde. Dit om een eventuele afwijking in phiW te compenseren. Bij vlakke stroming is de grenswaarde minder strikt en is er (afhankelijk van de situatie) geen veiligheidsmarge nodig. In de praktijk is gebleken dat (vooral bij vlaksymmetrische stroming) ook bij minder steile conushoeken massastroming kan optreden bij voldoende vulhoogte van het stortgoed in de cilinder. Bij silo-ontwerp wordt hier meestal geen rekening mee gehouden en worden de grenswaarden gebruikt die ook bij kleinere vulhoogten tot massastroming leiden. Invloeden stromingspatroonIn veruit de meeste gevallen is massastroming gewenst. Daarom loont het de moeite de silo zo te ontwerpen, dat dit type stroming gewaarborgd is. Het stromingspatroon dat optreedt in een silo, wordt bepaald door:
Hierbij kan in zijn algemeenheid worden gesteld dat massastroming wordt bevorderd door een steilere en gladdere trechter. De wanden en hoeken moeten daarom glad afgewerkt zijn. Verder is een trechter met een sleufvormige opening beter dan een ronde of vierkante trechter. Procedure massastroom-ontwerpHet ontwerp van een massastroomtrechter verloopt als volgt:
Ontwerp op brugvormingDat er bij een goedgekozen hellingshoek van de trechter massastroming optreedt, wil niet zeggen dat er in alle gevallen stroming op zal treden. Wanneer de opening te klein is, zal er brugvorming optreden, zodat er helemaal geen stroming zal zijn. Na de keuze voor de geschikte conushoek voor massastroming komt dus de uitstroomopening in beeld. De voornaamste storingsbron bij massastroming is de vorming van min of meer stabiele productbruggen die de stroming belemmeren of zelfs geheel laten stoppen. 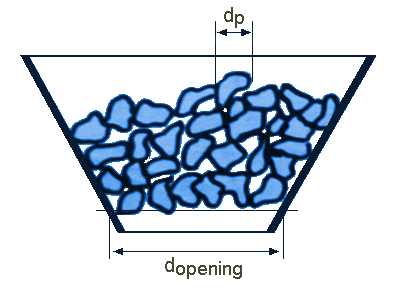
Verklemming van grote brokkenIn het geval van vrij stromende (meestal wat grovere) materialen gaat het dan meestal om een mechanische verklemming van een aantal deeltjes direct boven de opening. Door de kleinste afmeting van deze opening tenminste vijf of zeven maal groter dan de grootste productdeeltjes te kiezen, wordt dit voorkomen. Cohesieve brugvormingIn het geval van cohesieve producten gaat het om de samenbakking van zeer veel deeltjes die tot stabiele gewelven of bruggen kan leiden.
In dit geval komen we er niet met simpele vuistregels, maar is een nadere beschouwing nodig.
Zie hiervoor onderstaande figuur, waar de factoren zijn uitgezet die bij brugvorming in een silo een rol spelen.
Tengevolge van deze spanning sigma1 krijgt het (cohesieve) materiaal een zekere eigen sterkte sigmaP, die afhankelijk is van de grootte van sigma1. Denk hierbij aan een sneeuwbal: hoe harder we er in knijpen, hoe sterker hij wordt. We kunnen de eigensterkte sigmaP beschouwen als de weerstand die het betreffende materiaal biedt tegen vervorming, afhankelijk van de plaats in de silo.
Vervolgens beschouwen we het product in de silo (of eigenlijk voornamelijk in de trechter) alsof het is opgebouwd uit een serie boven elkaar
geplaatste bruggen of bogen die afsteunen op de silowand en waarbij elke brug minimaal zijn eigen gewicht draagt.
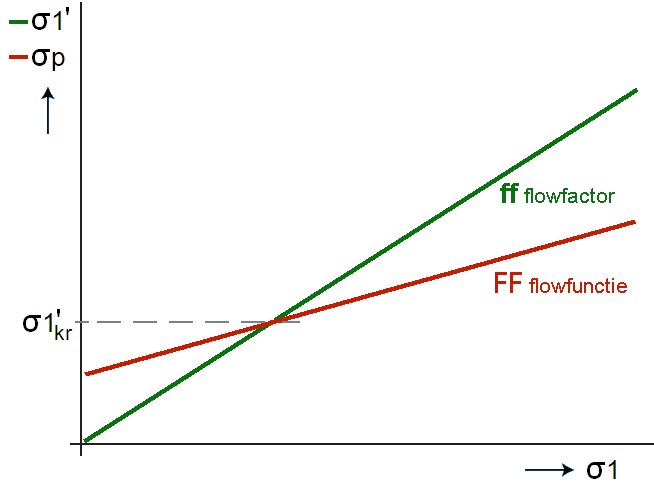
Flow – No FlowUit de klassieke silotheorie volgt dat de verhouding tussen consolidatiespanning sigma1 en de benodigde brugsterkte sigma1' voor een bepaalde combinatie van stortgoed en silotrechter (weergegeven door alfa, phiW en phiE) een constante waarde heeft. Deze factor wordt de flow-factor (ff) genoemd. Uitgezet in een grafiek levert dit dus een rechte lijn, onder een zekere hoek met de x-as. Deze waarde kan voor een specifiek geval uit de theorie worden berekend of grafisch afgelezen. Het verband tussen consolidatiespanning sigma1 en eigensterkte sigmaP, is puur een producteigenschap en dient met een geschikte tester te worden gemeten. Dit verband wordt aangeduid als Flow-Functie FF. Beide lijnen zijn in de figuur uitgezet, en weer geldt dat een brug niet stabiel is zolang de benodigde brugsterkte (ff) groter is dan de materiaalsterkte (FF), hetgeen het geval is rechts van het snijpunt van beide lijnen. Het snijpunt van ff en FF geeft precies de plaats aan waar de situatie kritiek is. Uit de hierbij behorende kritische waarde van sigma1' kan rechtstreeks de bijbehorende kritische uitstroomopening van de trechter Dkr worden berekend. In de praktijk kiezen we hierop meestal een toeslag van 25% voor de werkelijk toe te passen, minimale opening. Sterkte van de brugHet product in de silo zal druk ondervinden van het bovenliggende product. Door deze silodruk krijgt het product een zekere samenhang, de eigensterkte.
Vergelijk dit met het vormen van een sneeuwbal en een "zandbal"; met droog zand is het laatste niet mogelijk.
Vooral de laatste speelt in veel situaties een rol, zoals vaak blijkt uit de opstartproblemen na een weekend. Dit wordt veroorzaakt door consolidatie.
Om de sterkte van een brug te kunnen berekenen moet de eigensterkte van het product als functie van de druk gemeten worden. Zie meting tijdsbezwijklijn.
Procedure brugvormingBij dit gedeelte van het silo-ontwerp wordt de diameter van de opening vastgesteld om het product probleemloos uit te laten stromen. De procedure is als volgt:
Soms is de opening benodigd voor stroming, te groot om praktisch toepasbaar te zijn. Aan de hand van de beschikbare gegevens kan een gerichte oplossing gezocht worden:
Zo kan afhankelijk van de situatie met de ontwerpmethode en ondersteunende tests de optimale oplossing gevonden worden. Stromingsbevordering (flow promotion)Soms is de benodigde uitstroomopening erg groot. Bij producten met een lage bulkdichtheid en grote cohesiviteit of hakerigheid, kan (na stilstand) brugvorming optreden tot meerdere meters overspanning.
Bij lichte, hakerige producten is 3 tot 5 meter geen uitzondering. Er zijn zelfs gevallen bekend van bruggen met een overspanning van 9 meter.
In deze sitautie werd het product onttrokken door een heen en weer bewegend glijraam van 5 meter. De trechter was echter leeg tot een diameter van 9 meter.
Indien een grotere kritische diameter wordt gevonden dan een praktisch toepasbare opening dan zal hiervoor een oplossing moeten worden gezocht. Er zijn globaal twee oplossingsrichtingen:
Brugbrekers
Er is een keur aan brugbrekers (flow promotion devices) op de markt. Er wordt wel eens gezegd: je kunt het zo gek niet bedenken of het is al eens bedacht (en toegepast).
Brugbrekers worden vaak toegepast op bestaande silo's, waar (na stilstand) blijkt dat het stortgoed niet uitstroomt. Aanpassen van trechtervorm, trechterhoek of uitstroomopening is dan niet mogelijk of zeer ingrijpend. Het is dan relatief eenvoudig om een flow promotor te installeren, zeker als dat aan de buitenkant van de silo kan. Let op: bij toepassing van trillers om mogelijke bruggen te breken mag alleen worden getrild wanneer product kan uitstromen. Anders verslechtert de situatie misschien juist doordat de trillingen het product nog meer verstevigen. Uitdraagbodems
Een andere manier om stroming te waarborgen is een uitdraagbodem toe te passen, die de minimale uitstroomopening heeft.
De grootte van de bodem, c.q. het bewegende deel, is daarbij de maat voor de opening die het stortgoed "ziet".
De opening onder in de bodem kan dan duidelijk kleiner zijn.
UitdraagapparatuurIn het voorgaande is de trechtervorm en hellingshoek besproken. Voor de gewenste massastroming moet de trechtergeometrie goed zijn.
Het is echter niet genoeg; een andere vereiste is dat de stroming niet verstoord wordt door onderliggende obstakels of apparatuur.
Uitdraagschroef (doseerschroef, screw feeder)In het voorgaande kwam ter sprake dat een wigvormige trechter gunstig is voor het optreden van massastroming. Nadeel is dat er een sleufvormige opening ontstaat, hetgeen extra eisen stelt aan de uitdraag-apparatuur. Deze apparatuur moet voor een gelijkmatige onttrekking zorgen. Is dit niet het geval dan zal de feeder kernstroming veroorzaken, ook al is de silo op massastroming ontworpen. Richtlijnen voor uitdraagapparatuurHoewel voor deze apparatuur niet een alles omvattende theorie bestaat zijn een paar aandachtspunten te geven waar bij het ontwerp en dimensionering op gelet moet worden.
Zie ontwerp van een doseerschroef voor een praktijkvoorbeeld waarbij een schroef is ontworpen die er voor zorgt dat product over de hele opening wordt onttrokken. Silo-ontwerp en productverstevigingDe invloed van tijdsconsolidatieIn het vorige hoofdstuk kwam een standaardmethode aan bod voor het ontwerpen van massa-stroomsilo's. Daarbij zijn een aantal zaken die invloed uitoefenen op het ontwerp of op het gebruik van de silo nog niet aan de orde geweest. In dit hoofdstuk gaan we daarop in en geven we aan hoe hiermee bij het ontwerp of bij het gebruik rekening kan worden gehouden. Maandagochtendhumeur
Sommige opslagsilo's lijken last te hebben van een maandagochtendhumeur. Vrijdagmiddag loopt de zaak nog uitstekend,
maar wanneer maandagochtend na een ongestoord weekend de zaak weer wordt opgestart, komt er geen product uit de silo.
Slechts door een paar forse klappen met een voorhamer op de trechter komt de stroming dan soms weer op gang.
TijdsflowfunctieWaar we eerder het gemeten verband tussen consolidatiespanning (sigma1) en eigensterkte (sigmaP) aangaven met de flowfunctie FF, hebben we bij de tijdsinvloed te maken met de tijdsflowfunctie FFt. Belangrijk is in deze ook de duur van de ongestoorde opslag, daar een langere tijd ook meestal tot een grotere sterkte zal leiden. We zullen dus voor tijdsgevoelige producten al bij het ontwerp van de silo een indruk moeten hebben of en hoe lang het product wordt opgeslagen zonder dat er product aan de silo wordt onttrokken. 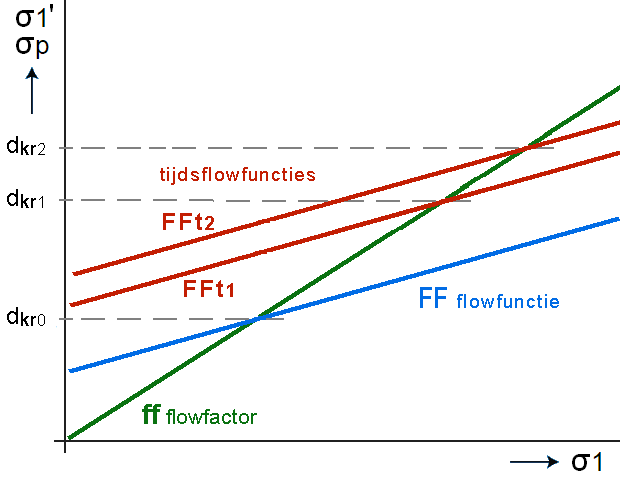
Uitstroomopening na stilstandIn de praktijk zal na een periode van stilstand de sterkte van het product meestal groter zijn. Dit komt tot uitdrukking in de flowfunctie, zie figuur hierboven. We zien hier in de eerste plaats de flowfactor (groen) en de flowfunctie zonder stilstand (blauw). Het snijpunt van beide lijnen leidt tot de kritische waarde van de brugsterkte, waaruit de kritische uitstroomopening d_kr0 wordt berekend. Zie ontwerp brugvorming Verder zien we in de figuur twee tijdsflowfuncties (rood), gemeten voor een zekere ongestoorde opslagtijd, bijvoorbeeld 1 dag en 4 dagen. De snijpunt van deze tijdsflowfuncties met de flowfactor leiden tot een hogere waarden voor de kritische uitstroomopening. Ontwerp met stilstand
Door te kiezen voor een grotere uitstroomopening, kunnen we dus rekening houden met het tijdseffect en zal ook na stilstand de silo weer probleemloos op gang komen.
Consolidatie brekenDe eerste mogelijkheid is om uit te gaan van een realistische opening, bijvoorbeeld de opening die nodig is als het product niet stilstaat en verstevigd, met een veiligheidstoeslag. We accepteren dan dat er na stilstand stabiele brugvorming over de uitstroomopening kan optreden, en passen een geschikt hulpmiddel (bijv. een triller, klopper, luchtinjectie of luchtkanon) toe om deze bruggen te breken. Zodra stroming optreedt, vindt er voldoende vervorming in het product plaats om de tijdsinvloed op te heffen zodat verdere stroming zal optreden zonder hulpmiddelen. Uitdraagbodem
Een andere manier om stroming te waarborgen is een uitdraagbodem toe te passen. De diameter van de bodem, c.q. het bewegende deel, moet dan zo groot zijn als de benodigde opening.
Wanneer de bodem in werking is, moet deze het storgoed over het gehele oppervlak afvoeren. Of dit voor een bepaald product echt werkt moet eventueel in de praktijk worden getest.
Consolidatie voorkomenEen andere mogelijkheid is om uit te gaan van de kritische opening, behorende bij een bepaalde tijdsduur, bijv. zes uur ongestoorde opslagtijd, en ervoor te zorgen dat geen langere stilstandtijden optreden. Hiervoor moet er steeds voor zes uur stilstand wordt bereikt een relatief kleine hoeveelheid product (als vuistregel: een halve trechterinhoud) worden afgetapt en gerecirculeerd (of afgevoerd). Dit herstelt de tijdloze situatie en zo kan stroming verder zonder hulpmiddelen plaatsvinden. Welke van deze mogelijkheden de voorkeur verdient, zal per situatie verschillen maar kan op basis van de te meten tijdsinvloed op het betreffende product worden beoordeeld. Zie ook stromingsbevordering. Productversteviging en stromingspatroonDe productversteviging tijdens stilstand zal in het algemeen geen invloed hebben op het stromingspatroon. Wanneer de stroming weer op gang komt, al dan niet met hulpmiddelen, zal hetzelfde stromingpatroon optreden. Slechts in uitzonderlijke situaties, bijvoorbeeld wanneer tijdens stilstand het product echt aan de wand koekt of blijvende klonten vormt, kunnen problemen optreden. Dit aankoekgedrag komt meestal bij de metingen in de ontwerpfase naar voren. Keuze voor een ander wandmateriaal, bijvoorbeeld RVS of een geschikte coating, biedt dan soms een oplossing. Invloed van het onttrekmechanisme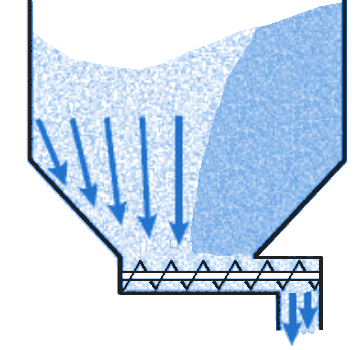
Direct onder de uitstroomopening van een silo bevindt zich meestal een onttrekmechanisme (feeder).
Dit is een kort transportmiddel dat de productstroom uit de silo regelt. Vaak toegepaste feeders zijn schroef-, band- en trilfeeders.
Voor een goede werking van de silo is het van belang dat de feeder product onttrekt over de gehele uitstroomopening.
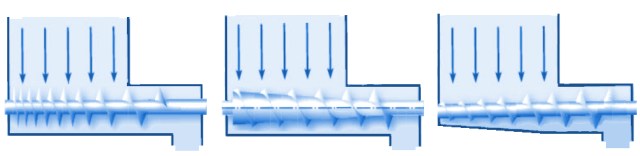
Case uitdraagschroef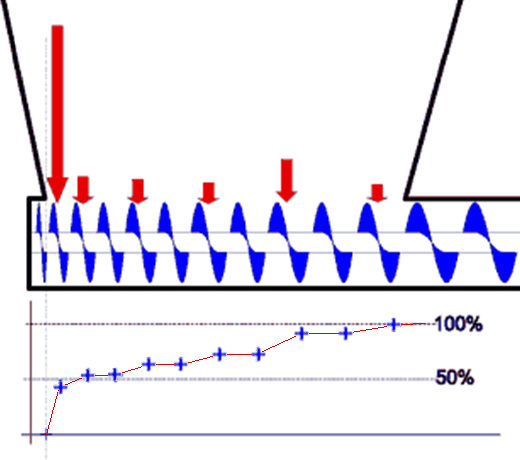
Een silo voor hout- en gipspoeder gaf regelmatig stromingsproblemen. Dit uitte zich in stagnatie van de stroming.
Onder de silo zat een uitdraagschroef met een verlopende spoed.
Brugvorming in de cilinder
Niet alleen in de trechter komt brugvorming voor. Soms vormen zich ook min of meer stabiele gewelven in de cilinder/ het verticale deel van de silo.
Dat komt dan meestal door tijdsconsolidatie.
Wanneer het product onder het gewelf wel normaal uitstroomt, vallen dergelijke brugvorming niet direct op. Maar op het moment dat dan
een dergelijk gewelf bezwijkt, spontaan of door externe trillingen, storten vaak tonnen product omlaag en leiden tot ernstige schade.

In de praktijk komen stabiel gewelven in de cilinder het meest voor in relatief nauwe (rechthoekige) cellen met damwanden. Over het algemeen zal brugvorming in de trechter eerder optreden dan in de cilinder. Wanneer het opslagproduct echter gevoelig is voor tijdsversteviging, is controle hierop geboden. Zeker bij toepassing van stromingsbevorderende hulpmiddelen de trechter. Als het optreden van hang-ups niet kan worden uitgesloten, verdient het aanbeveling om niveaumeters in de silo aan te brengen die een probleem tijdig signaleren, om schade te voorkomen. Silo’s met kernstromingStroomkanaal bevindt zich in product zelf bij kernstroomsiloDit is het derde hoofdstuk over silo-ontwerp. In het eerste deel werd het basisontwerp beschreven van silo’s met massastroming. Het tweede deel behandelde de invloed van stilstand (tijdversteviging). Dit artikel gaat over de situaties waar massastroming niet mogelijk of gewenst is. Hiervoor zal een kernstroomsilo ontworpen moeten worden. Kernstroming versus massastroming
De voordelen van massastroming zijn dat er geen veroudering of bederf optreedt, omdat er geen stilstaande gebieden (dode zones) zijn.
Verder is de stroming goed regelbaar, bestaat er weinig kans op ontmenging en treedt first-in, first-out op, hetgeen traceerbaarheid mogelijk maakt.
Nadelen van massastroming zijn de benodigde steile trechter die bouwhoogte kost en de slijtage van de silowand die kan optreden bij abrasieve producten.

Kleinere bouwhoogte
Ondanks de minder aantrekkelijke eigenschappen kan een kernstroomsilo in een aantal gevallen toch een goede opslagmogelijkheid bieden.
We kunnen hierbij denken aan producten waarvoor bederf, veroudering of ontmenging geen rol spelen.
Of producten met een zodanig hoge wandwrijving dat een absurd steile trechter nodig zou zijn voor massastroming.
Stabiele schachtvorming vermijdenIn kernstroomsilo’s kan bij cohesieve producten onder ongunstige situaties een zogenaamde stabiele schacht ontstaan. Hierbij stagneert de verdere uitstroming van product na het leegstromen van dit stroomkanaal. De diameter van een dergelijke stabiele schacht zal nagenoeg gelijk zijn aan de grootste afmeting van de uitstroomopening. Op basis van de silotheorie en de producteigenschappen kan de kritische waarde van de uitstroomopening worden bepaald waarbij geen stabiele schachtvorming zal optreden.
Analoog aan het flow/no-flow criterium bij massastroomsilo’s kan ook hier voor de schacht een verstevigingsspanning (sigmaP) worden bepaald
met een bijbehorende eigensterkte van het product in de schachtwand. Verder kan de grootste hoofdspanning (sigma1) werkend op de wand van de schacht worden berekend.
Bovengrens stabiele schachtvorming
Hierbij gaan we er van uit dat de grootste hoofdspanning (sigma1) gelijk zal zijn aan de verticale spanning op de beschouwde diepte in de silo.
Voor gedrongen silo’s, met een hoogte/diameter verhouding kleiner dan 1 kan hiervoor de ongesteunde stortgoeddruk worden genomen,
berekend als bulkdichtheid maal gravitatieversnelling maal vulhoogte (sigma1 = rho * g * H ).
De bij sigma1 behorende waarde van de eigensterkte (sigmaP) kan uit de gemeten flowfunctie van het product worden bepaald.
In de meeste gevallen zal hiervoor de tijdsflowfunctie moeten worden gekozen, omdat het product in de schachtwand langere tijd onder druk stilstaat,
zelfs al is de schacht niet stabiel. Uit de voorwaarde dat de schachtbelasting (sigma1’) kleiner moet zijn dan de eigensterkte volgt dan de benodigde diameter van de schacht,
(c.q. de breedte van een spleetvormige opening, of de diagonaal van een rechthoekige opening), waarboven geen stabiele schacht zal ontstaan.
Ondergrens stabiele schachtvorming
Deze berekeningswijze van de verstevigingsspanning wordt nog wel in wat oudere literatuur gevonden.
Als uitgangspunt geldt dat de grootte van de grootste hoofdspanning (sigma1) niet afhankelijk is van de hoogte van het product
in de silo maar wordt bepaald door de spanning op de schachtwand tengevolge van het eigen gewicht van het product binnen de schacht.
Op basis van de producteigenschappen en wat vereenvoudigingen kan dan een flowfactor voor schachtvorming ff worden berekend.
Controle op brugvorming
Naast het feit dat er geen stabiele schacht mag blijven staan, mag er in het stroomkanaal geen brugvorming optreden.
Bij een spleetvormige opening zou brugvorming over de kleinste afmeting op kunnen treden en is controle wel nodig.
Dit gaat in principe op dezelfde wijze als bij massastroming, maar het probleem bij kernstroming is dat de uitstroming
niet langs de silowand maar in een in het product zelf gevormde trechter stroomt.
Hiervan is de hoek niet bekend. In feite is hierdoor de grootte van de flowfactor niet bekend,
doch in de praktijk wordt hiervoor meestal de waarde ffp = 1,7 gekozen, overeenkomend met een interne,
halve trechterhoek van 30 graden.
Trechterhoek voor leegstromen
In veel gevallen zal het nodig zijn dat een kernstroomsilo volledig leegstroomt.
Bijvoorbeeld wanneer meerdere producten afwisselend moeten worden opgeslagen of bij de kans op bederf in de dode zones.
Theoretisch kan volledig uitstromen optreden wanneer de helling van de trechter iets groter is dan de wandwrijving tussen stortgoed en wand.
In de praktijk wordt daarom aanbevolen om voor volledig uitstromen een trechterhoek met de verticaal (alfa) zo te kiezen, dat de som van trechterhoek en wandwrijvingshoek (phiW) maximaal 65 graden is (ofwel: α + phiW ≤ 65°) te kiezen. 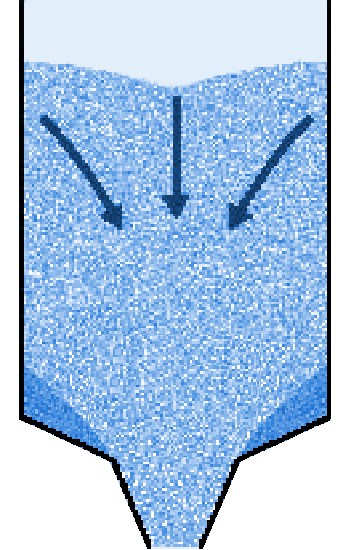
een kernstroom-deel en een massastroom-deel Extended flow hopper
Soms is het zinvol om een combinatie van een massastroom- en een kernstroomsilo toe te passen (zgn. extended flow).
Hierbij wordt het bovendeel ontworpen voor kernstroming en het onderste gedeelte als massastroomtrechter zie figuur.
Het kernstroomgedeelte moet voldoende steil zijn om volledig te kunnen leegstromen en de overgangsdiameter moet groot
genoeg zijn om stabiele schachten te voorkomen.
Platbodemsilo’s of stockpiles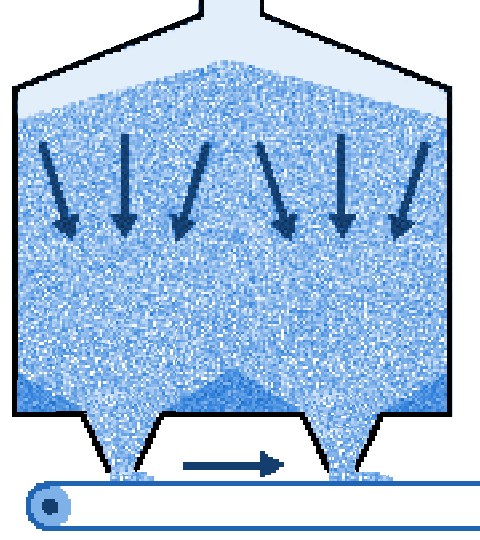
Ook bij de inbouw van reclaimhoppers onder platbodemsilo's of stockpiles kan op deze wijze stabiele
schachtvorming worden voorkomen.
Dat levert dan bij een goede positionering ook voldoende vrijstromend product op.
Probleemloos doseren met een doseerschroefOntwerp op basis van minimale spoed, kerndiameter en spoedverloopBij het uitdragen en doseren van poeders uit een silo of bunker worden vaak schroeven toegepast. Dit heeft een aantal voordelen, waaronder het vermijden van vervuiling van poeder en omgeving, een goede dosering en een groot capaciteitsbereik. Bovendien heeft een langwerpige opening voordelen met betrekking tot de stroming van het product. Als een uitdraag- of doseerschroef echter niet goed ontworpen is, dan kunnen kernstroming of brugvorming optreden. Ook bestaat het risico dat het product doorschiet en onbeheersbaar uitstroomt (flooding) of kan de schroef op sommige punten overmatige slijtage te zien geven. Een goed ontwerp, waarbij spoed en kerndiameter zijn afgestemd op de eigenschappen van het product, voorkomt deze problemen. 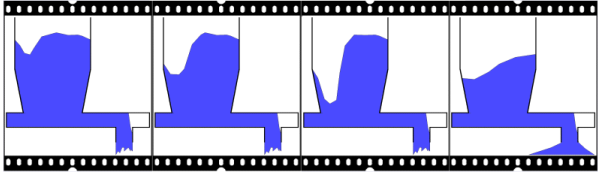
InleidingIn een proces worden diverse stoffen aangevoerd of toegevoerd. Grondstoffen worden vaak gebruikt in de vorm van bulkgoed, maar ook bij processen met voornamelijk vloeistoffen of gassen moeten regelmatig poedervormige stoffen worden toegevoerd. De dosering is hierbij van groot belang. Te veel of te weinig veroorzaakt een slechte kwaliteit van het eindproduct. Ook al betreft het een goedkoop vulmiddel, stagnatie kan tot hoge kosten leiden, omdat het proces gedurende een bepaalde tijd niet de gewenste productie levert. De silo of bunker waarin het poeder wordt opgeslagen, verdient daarom de nodige aandacht. In een dergelijke bunker moet massastroming optreden (zie silo-ontwerp), omdat kernstroming nadelen heeft met betrekking tot stroming, veroudering en productdegradatie. Verder mag in een bunker natuurlijk geen brugvorming optreden. Aan een proces toegevoegde poeders zijn dikwijls zeer fijn en adhesief. Vaak hebben ze een groot specifiek oppervlak of een open korrelstructuur, om opname of reactie goed te laten verlopen. 
Dit leidt ertoe dat deze poeders slechte stromingseigenschappen hebben. Om deze redenen is toepassing van een wigvormige trechter (een trechter met twee verticale wanden) gewenst. Zowel wat betreft het stromingspatroon als brugvorming biedt dit type trechter voordelen ten opzichte van een ronde of vierkante trechter. Het is dan wel van groot belang dat het poeder over de volle lengte aan de opening wordt onttrokken. Hier kan een uitdraagschroef goede diensten bewijzen. 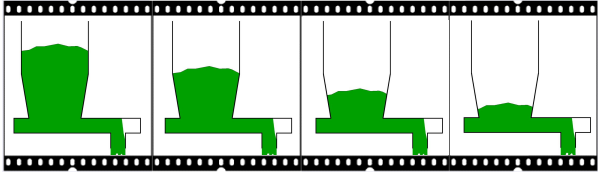
UitdraagschroefEen uitdraagschroef (oftewel een doseerschroef, doseervijzel of screw feeder) is een schroef die direct onder de silo-opening is geplaatst. Het product in de silo staat dan op een deel van de schroef. De uitdraagschroef is (werkt) daarom duidelijk anders dan de transportschroef, waar het product wordt toegevoerd met een capaciteit die kleiner is dan van de schroef, die daardoor nooit voor 100 procent is gevuld. Een uitdraagschroef wordt veel toegepast voor het doseren van poeders uit een (wigvormige) trechter. De redenen hiervoor zijn:
Willen deze voordelen echter gelden, dan is een goed ontwerp van de schroef noodzakelijk. Werkingsprincipe schroeftransportHet transport door een schroef (of vijzel) komt tot stand door de wrijving van het product met de
goot eromheen. Het werkingsprincipe komt overeen is te illustreren met dat van een wenteltrap. Een
voorbeeld: een proefpersoon staat op een bepaalde trede van een wenteltrap. Als deze trap wordt
rondgedraaid, dan draait hij op dezelfde hoogte rond. Als de proefpersoon echter tegen de muur gaat
staan die rondom de trap is gebouwd is, en als de trap gaat draaien, dan verandert de situatie. Er
zijn twee opties: 1) de persoon blijf staan, waardoor de muur horizontaal langs hem heen schuurt. Of 2)
hij blijft op dezelfde positie tegen de muur staan. Hij moet dan wel telkens een stapje omhoog. Vertaald naar een schroef betekent dit dat het transport afhankelijk is van de wrijving tussen het product en het schroefblad, het product en de goot of buis en de wrijving van het product zelf (in het deel onder de silo). De hoogte van de treden komt tot uitdrukking in de bladhoek. Die wordt gevormd door de spoed en de schroefdiameter. Verder is ook de kerndiameter (de diameter van de as waarop de bladen zijn bevestigd) van belang, omdat deze de inhoud van een gang bepaalt. 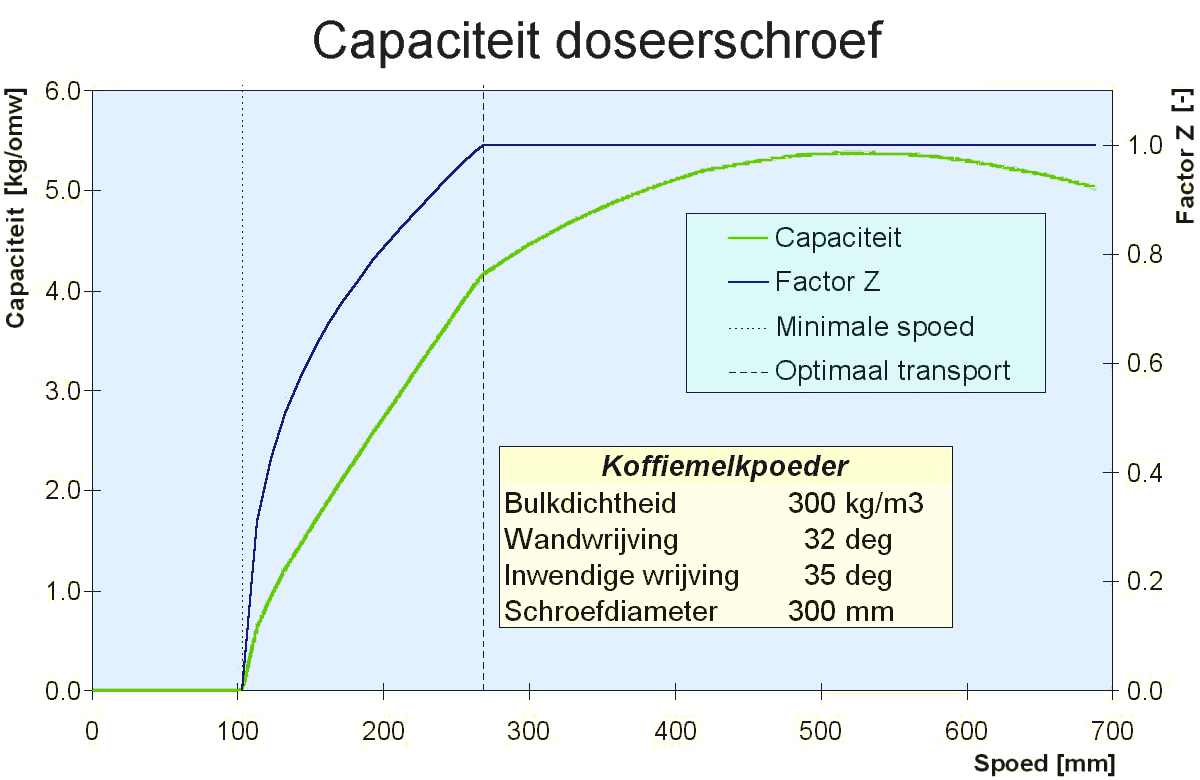
SpoedBij het capaciteitsverloop van een uitdraagschroef zijn er drie belangrijke punten:
De ligging van deze punten is afhankelijk van kerndiameter, schroefdiameter en producteigenschappen. ad 1 Ondergrens minimale spoedIs de toegepaste spoed kleiner dan de minimale spoed, dan zal het product tussen de bladen ingeklemd blijven zitten en draait het product mee. De kerndiameter speelt hierbij ook een rol. Is deze groter, dan is het bladoppervlak kleiner. De minimale spoed wordt daarmee groter. Verder is de wandwrijving en de inwendige wrijving van belang. In tabel 1 zijn waarden voor minimale spoed (ondergrens) berekend. Hierbij is de wrijving tussen product en goot en product en schroefblad gelijk verondersteld. Bij een spoed groter dan minimaal, het gebied tussen 1) en 2) wordt de effectiviteit van transport uitgedrukt in de factor Z. ad 2 Bovengrens minimale spoedDe spoed waarboven de werking optimaal is wordt de bovengrens van de minimale spoed genoemd. Net als de ondergrens van de minimale spoed hangt de waarde af van de schroefafmetingen en de productgegevens. Boven deze bovengrens neemt de capaciteit in eerste instantie vrijwel lineair toe met de spoed. Bij een steeds groter wordende spoed echter, stijgt de capaciteit minder. Bij het ontwerp is dit laatste deel niet te gebruiken. Als de capaciteit minder toeneemt dan de positie op de schroef verlangt, heeft vergroting van de spoed geen effect meer. ad 3 Maximale spoedBoven een maximale spoed loopt de capaciteit terug. Het schroefblad glijdt dan onder het product door. In het ontwerp mag een spoed groter dan deze niet voorkomen. Gebeurt dat wel, dan is de situatie vergelijkbaar met een verkleining van de spoed. Hiervan is bekend dat dit leidt tot verklemming. Het benodigde vermogen schiet omhoog, wat kan resulteren in beschadiging van de schroef. 
Ontwerp uitdraagschroefBij het ontwerp van een uitdraagschroef is het doel de capaciteit van de schroef gelijkmatig over de lengte te laten toenemen. De ontwerpprocedure verloopt als volgt: De wandwrijving op het materiaal van goot en schroefblad en de inwendige wrijving van het product worden gemeten. Vervolgens wordt het capaciteitsverloop rondom de maximale spoed berekend. Aan de hand hiervan wordt vastgesteld wat de maximaal toe te passen spoed mag zijn. De gewenste capaciteit en de spoed bepalen vervolgens het toerental, de schroefdiameter en de kerndiameter bij de uitstroom. Dit bepaalt de toename van de capaciteit per lengte van de schroef. Daarna kan de invulling van de kerndiameter en de spoed plaatsvinden. Als eerste wordt de begin-kerndiameter gekozen, die bij korte schroeven in sommige gevallen hetzelfde kan zijn als de kerndiameter aan het eind. Vervolgens wordt de minimale spoed berekend en wordt de beginwaarde van factor Z gekozen. Het sprongetje in capaciteit dat hierdoor ontstaat wordt eventueel weggewerkt met een extra stukje gang met de beginspoed. De spoed neemt toe totdat optimaal transport wordt bereikt. Als de kerndiameter in het begin groter is dan aan het eind, wordt de afname van de as bepaald. In het laatste deel neemt de spoed weer toe, tot aan de eerder bepaalde maximale waarde bij het verlaten van de bunker. In de transportsectie van de schroef (na de bunker) neemt de spoed nog iets toe, om de vulgraad te verminderen. Het resultaat van deze procedure is een (bijna) gelijkmatige onttrekking van het product over de lengte van de schroef. Hierdoor zullen er geen stilstaande gebieden in de silo zijn -- mits de silo goed is ontworpen -- en is de kans op brugvorming en doorschieters minimaal. 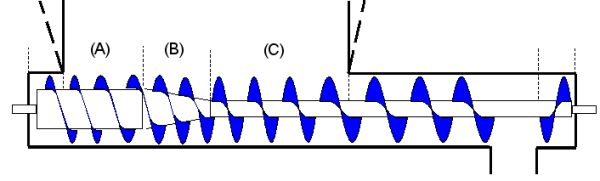
Bij een tamelijk lange invoersectie, zoals bij een grotere silo het geval zal zijn, zal de doseerschroef
uit drie secties bestaan. Eerst (A) een deel waarbij de kerndiameter groter wordt gekozen,
zodat de beginspoed redelijk klein kan blijven. Vervolgens (B) een deel waarbij de kern verloopt, en
de spoed meestal hetzelfde blijft. Tot slot het deel met een minimale kerndiameter, en toenemende spoed (C).
Vermogen doseerschroefAan de hand van de afmetingen van de schroef, het spoedverloop en de producteigenschappen kunnen ook het benodigde aandrijfmoment en -vermogen worden berekend. Hier komt het verschil tussen uitdraagschroef en transportschroef duidelijk naar voren. Door de grotere vulgraad van de uitdraagschroef (onder de silo 100 procent en daarna vaak minstens 80 procent) en doordat er in het deel onder de silo een druk wordt uitgeoefend op het product in de schroef, zijn het benodigde aandrijfmoment en -vermogen duidelijk hoger dan bij een transportschroef. Hiermee moet dus terdege rekening gehouden worden bij de keuze van de aandrijving. Aan de hand van afschatting van de silodruk bij stilstand van de schroef kan ook een aanloopmoment worden vastgesteld. Dan kan worden onderzocht of de motor, de reductor en eventueel de frequentieregelaar dit kunnen opbrengen. 
Uitstroomcapaciteit uit silo’sBerekening van de uitstroomhoeveelheid van poeders en korrelsBij het bepalen van de benodigde afmeting van de uitstroomopening van een silo is naast de minimumafmeting om brugvorming te voorkomen, ook de gewenste uitstroomcapaciteit van belang. In tegenstelling tot vloeistofstroming is dit debiet bij stortgoed niet eenvoudig te voorspellen, omdat vele factoren een rol kunnen spelen. Hoewel in vele praktische toepassingen de regeling van het massadebiet zal plaatsvinden door geschikte uittrekmechanismen als sluizen of schroeven, zal de silo zelf toch tenminste de maximaal gevraagde hoeveelheid moeten kunnen leveren via de uitstroomopening. 
Al sinds het midden van de 19e eeuw is (meestal empirisch) onderzoek gedaan naar de uitloopsnelheid van stortgoed uit silo’s/trechters. Tot op heden is geen eenduidige theorie of benadering bekend waarmee voor alle typen stortgoed en uitloopgeometrie het debiet nauwkeurig kan worden voorspeld. Wel zijn voor diverse klassen van stortgoed empirische of theoretische benaderingen afgeleid waarmee binnen de geldigheidsgebieden het debiet kan worden berekend. Een aardig voorbeeld van het uitstromen van deeltjes wordt gegeven in de bekende zandloper, zoals te zien in afbeelding 1. De schijnbaar rustige en mooie materiaalstroom blijkt bij nadere beschouwing eigenlijk helemaal niet zo netjes. De deeltjes botsen en rollen over elkaar bij de uitstroomopening, soms stokt de zaak zelfs even en treden er grote snelheidsverschillen tussen de deeltjes op. Toch levert dit geheel een zeer betrouwbare en reproduceerbare tijdmeting op die zich al zeer lang heeft bewezen. Maar ondanks dat is ook hier de uitstroomtijd niet te voorspellen en is eenmalige ijking noodzakelijk. Uitstroomdebiet voor grofkorrelig vrijstromend bulkgoed
Naar het uitstromen van niet al te fijn en niet-cohesief bulkmateriaal is in het verleden veel onderzoek gedaan. Niet al te fijn betekent een deeltjesgrootte van meer dan 400 micrometer (0.4 mm). In de literatuur is een aantal empirisch bepaalde vergelijkingen te vinden.
Deze komen qua opbouw overeen, en bestaan uit de afmeting van de uitlaat minus de deeltjesdiameter vermenigvuldigd met een factor,
en dat tot een zekere macht en ook weer vermenigvuldigd met een zekere factor.

Een simpele benadering die vaak wordt gebruikt, is de empirische formule van Beverloo.
Beverloo vond in zijn metingen voor factor waarmee de deeltjesgrootte moet worden vermenigvuldigd, waarden van k = 1.3 tot k = 2.9.
Bij bolvormige deeltjes was dit k = 1.6. Uit de formule blijkt dat bij grotere uitstroomopeningen en kleine deeltjes de deeltjesgrootte niet meer van belang is.
Een mogelijke tekortkoming bij de benadering van Beverloo is dat er geen rekening wordt gehouden met de mogelijke invloed van de trechterhoek.
Voor trechters met massastroming laat vergelijking van de formules zien dat Lehmann het meest afwijkt van het gemiddelde van de verschillende theorieën. De formules van Beverloo zitten dichter bij het gemiddelde. Dat geeft reden te denken dat met de benadering volgens Beverloo een redelijke voorspelling van het uitstroomdebiet kan worden gegeven, mits deeltjes groter zijn dan 0.4 mm en het product vrijstromend is. Uitstroming bij fijne vrijstromende materialenBij vrijstromende producten met een significant aandeel deeltjes kleiner dan 0.4 mm, blijkt het uitstroomdebiet aanzienlijk kleiner dan wordt voorspeld met Beverloo. De oorzaak hiervan is de weerstand van tegenstromende lucht die belangrijker wordt naarmate de deeltjes kleiner zijn. Tijdens het naar beneden stromen in de conus, neemt de druk op het materiaal af waardoor expansie optreedt en de ruimte tussen de deeltjes toeneemt. Hierdoor daalt de luchtdruk tussen de deeltjes waardoor lucht zal toestromen via de uitstroomopening, dus tegen de korrelstroom in. De productlaag bovenin de trechter is namelijk veel dichter, en in de cilinder nog meer, zodat lucht daar niet snel doorheen kan stromen. Deze tegenstroom is afhankelijk van de drukgradiënt van de lucht in de conus, en deze gradiënt is weer afhankelijk van de silodruk in de conus, de compressibiliteit en permeabiliteit van het stortgoed, en is moeilijk te berekenen. 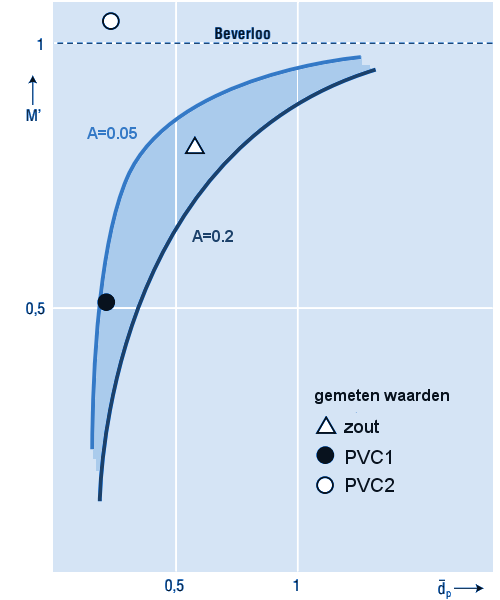
Een indruk van de afname van het debiet (berekend en gemeten door Thorpe en Nedderman) is te zien in afbeelding hiernaast. Hier is het debiet (als percentage van de Beverloo-voorspelling) gegeven als functie van de (dimensieloze) deeltjesdiameter. De getrokken lijnen geven de grenzen waartussen de meeste materialen zullen liggen, de meetpunten geven de resultaten weer van metingen aan drie industriële silo’s. Twee hiervan laten inderdaad een veel lager debiet zien dan bij grovere materialen zou optreden. Het derde is hoger dan de Beverloo-voorspelling hetgeen wordt veroorzaakt door een valpijp onder de silo. Door zo’n pijp wordt het stortgoed als ware uit de silo gezogen door het vallende product in de pijp. Opvoering van het debiet door luchtinjectie
Bij fijnkorrelige materialen bestaat nog de mogelijkheid om via injectie van lucht de drukgradiënt in de conus te verlagen en zo het debiet op te voeren.
Dit is een methode die werkt maar het resultaat is kwantitatief moeilijk te voorspellen.
Wel zijn op basis van modelproeven door Williams een aantal richtlijnen opgesteld.
Zo werd als beste positie voor het inbrengen van lucht een hoogte boven de opening van viermaal de uitstroomdiameter vastgesteld. Als beste resultaat werd een toename van het debiet met een factor 3 bereikt.
Debiet bij cohesief materiaalBij cohesief materiaal is het belangrijk de uitstroomopening tenminste zo groot te kiezen dat er geen stabiele brugvorming kan optreden. Meestal is de opening dan zo groot dat het gewenste uitstroomdebiet ruim gehaald wordt, en door een uitdraagapparaat wordt geregeld. Toch kan het ook hier nodig zijn om te weten wat de silo kan leveren. Johanson zette een benaderingsmethode op die nauw aansluit bij de ontwerpmethode van massastroomsilo’s voor cohesief materiaal gebaseerd op silogeometrie en gemeten materiaaleigenschappen. Hierbij gaat hij uit van continu bezwijkende bruggen in dynamisch evenwicht. 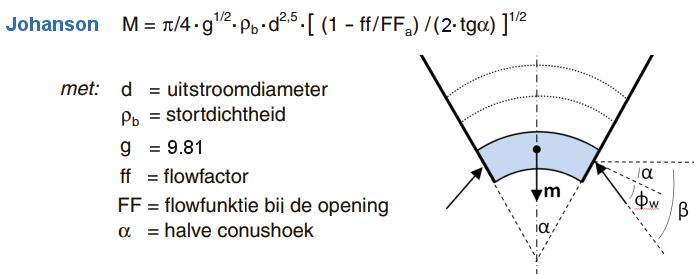
De drijvende kracht voor de stroming is het verschil tussen het eigengewicht van de brug en de wandreactie die weer samenhangt met de eigensterkte van het stortgoed. Uit zijn beschouwing kan een benadering voor het debiet worden afgeleid zoals hierboven weergegeven. De hierin benodigde waarden van de flowfactor ff en de flowfunctie FFa ter plaatse van de uitstroomopening zijn al bekend als de brugvormingseigenschappen van het product zijn gemeten om de diameter voor stroming te bepalen. Indien de methode van Johanson wordt toegepast op niet cohesief materiaal, dan vervalt de ff/FFa term en krijgt de vergelijking nagenoeg dezelfde vorm als de Beverloo-vergelijking. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||